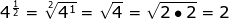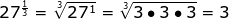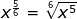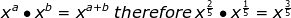Rational (Fractional) Exponents
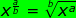

Now let's practice with a few numerical expressions.
A little more challenging
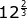
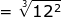
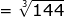
=
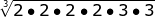
=
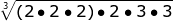
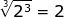
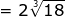
Now let's practice with a few variable expressions.
This is a little more challenging because the numerator is larger than the denominator.
-
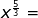
-
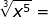
write as a radical expression
-
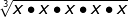 =
=
expand
-
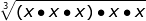 =
=
group triples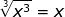 and you still have x2
and you still have x2
under the radical
-
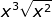
An easy way to remember the rule is to choose an example that you know for sure. For example
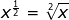 . This way you can remember that the denominator is the number that goes with the radical and the numerator goes with the number/variable under the radical.
. This way you can remember that the denominator is the number that goes with the radical and the numerator goes with the number/variable under the radical.Reminder: the exponent rules do not change when you are multiplying, dividing or raising a power to a power just because the exponent is a fraction.
To link to this Rational (Fractional) Exponents page, copy the following code to your site: