Zero Exponents
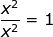 . If we look at the rules for division which says that when you divide you subtract exponents we get the following:
. If we look at the rules for division which says that when you divide you subtract exponents we get the following: 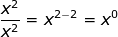 and since we already know that
and since we already know that 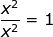 it follows that x° = 1 . This means that any number (except zero) raised to the zero power is 1.
it follows that x° = 1 . This means that any number (except zero) raised to the zero power is 1.Example 1: 3° = 1
Example 2: 12° = 1
Example 3: 101° = 1
Example 4: 31,456,236,719 ° = 1
Example 5: (-5)° = 1
Example 6: 0° =undefined ??? This is similar to dividing by zero. It is undefined.
Hmmm...Do you see an emerging pattern? We can write the rule as a° =1. You can remember it as any number (except zero) to the zero power is 1.
The most common mistake is to assume that the answer is zero. If you hesitate use your calculator to verify.
How does this apply when you are simplifying variable expressions that have an exponent of 0?
Example 7:
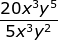
Rewrite
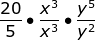
Subtract Exponents when you divide 4 •x3-3 y5-2
Simplify 4 •x° • y3
Zero exponent rule 4 • 1 • y3
Final result 4y3 therefore the x3canceled out
Let's think through this logically. We know that any number divided by itself is equal to one.
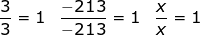
So it makes sense that any number to the zero power is one when we look at:
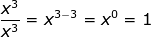
To link to this Zero Exponents page, copy the following code to your site:
