The laws of exponents are more just "tricks" or short cuts that help us work with exponents.

Recall that an exponent tells us to multiply the base a certain number of times.



Now, let's see how the laws can help us.



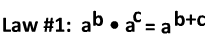
Why does this work? Let's use some numbers instead of variables to take a look.


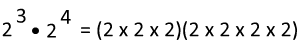
Because we are multiplying, we can get rid of the parentheses and now we have the problem



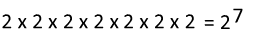
Here we can see that if we had simply just added the exponents 3 + 4 we would have still gotten 7.

This is also helpful when we are working with variables.



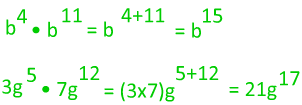
This law does not work unless the bases are the same.





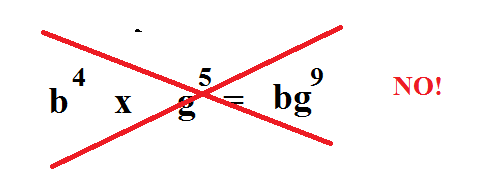
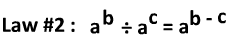
Let's take a look at why this law works:





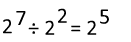
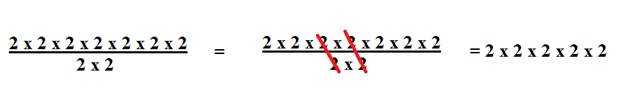
Here we can see that the twos on the bottom cancel out with some of the twos on top. We are left with 7 - 2 or 5 twos. So instead of having to cancel each time, we can just subtract the exponents.

This works with variables as well. Here are more examples:



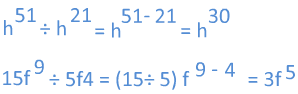
Notice that if there are numbers in front of the variable (coefficients), we just divide these as usual. Do not divide the exponents!



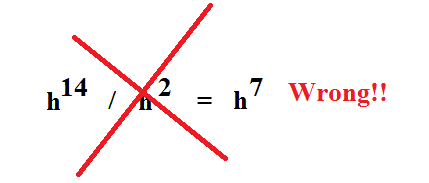
Let's Recap:

- For both Law #1 and Law #2, the bases must be the same.
- If there are coefficients, you follow the operation symbol.
- The exponents will be added if you are multiplying the bases and subtracted if you are dividing the bases.

Now, we have one more law to look at that will help simplify our work with exponents.



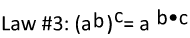
Again, we will use numbers to see how this works.



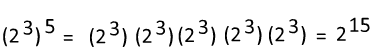
We can use Law #1 to simplify and see that 3 + 3 + 3 + 3 + 3 would be the same as 3(5).

This law is helpful when simplifying with variables also.



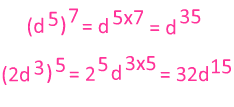
When we have a coefficient, we will still use the exponent as usual. The law only applies to the exponent part of the question.

These laws or short cuts can help make working with exponents a bit easier!