Remember that an exponent tells us how many times to multiply the base. Take a look at the pattern below:



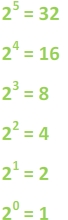
As you check out the pattern , you can see that each number is half as big as the previous one. In other words, you can take the number before, divide it by two and get the next number in the pattern. Let's use this pattern to help us explore negative exponents.











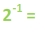
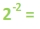
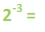
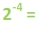
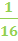
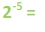
Now let's see if we can take the fractions and relate them back to the exponents. The denominators are the same numbers that we had in the first set of examples.







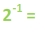
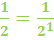
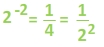
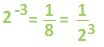
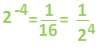
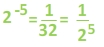
Here we can see a handy rule for working with negative exponents.



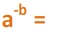
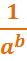
Now, we can rewrite an expression with a negative exponent and solve. Check out the examples below.

Examples:



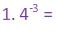
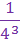
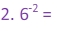
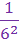
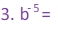
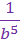
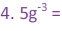
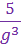
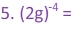
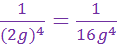
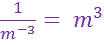
Notice the difference in the last two examples. In example 4, the exponent is only a power of g. However, in example 5, there are parentheses telling us that both the variable and the coefficient are raised to the exponent. So in example 4, the coefficient stayed on top of the fraction, but in example 5 the coefficient went0 on the bottom of the fraction.

Remember that negative exponents do not make negative numbers.

Let's Review:

When faced with a negative exponent, we can rewrite the expression by placing the base and exponent in the denominator of a fraction and making the exponent positive. Remember that negative exponents do not make negative numbers; instead that make fractions.