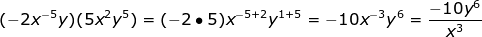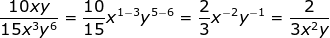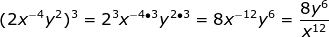Positive and Negative Integer Exponents
Let's start by reviewing the rules for exponents
I. Multiplying
When you multiply same bases you add exponents.
x4 •x5 = x4+5 = x9
What if an exponent is negative? Same thing add exponents.
x6 •x-4 = x6+(-4) = x2
What if there is more than one variable? Do each base separately.
(xy6)(x3y4) = x1+3 y6+4 = x4 y10
What if there is a coefficient in front of the variable?
3x2 •-2x3 =
(3 •-2)•(x2 • x3) = Use the commutative property to rearrange
-6x5 multiply the coefficients and add exponents
II. Dividing
When you divide same bases you subtract exponents
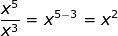
What if there is more than one variable? Do each base separately.
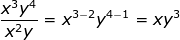
What if there is a coefficient in front of the variable? Divide the coefficients.
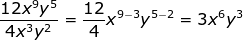
What if the exponent is negative?
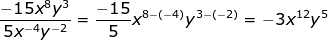
III. Raising a power to a power
When you raise a power to a power you multiply exponents.
(x3)5 = x3•5 = x15
What if there is more than one variable?
(x2y)3 = x2•3 y1•3 = x6y3
What if there is a coefficient?
(2x4y2)4 = 24 x4•4y2•4 = 16x16y8

IV. Negative exponent Rule
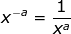
-
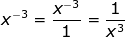 1st write with a "top floor" and "bottom floor"
1st write with a "top floor" and "bottom floor"
2nd change floors if the exponent is "unhappy"
-
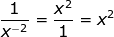 The exponent is unhappy in the denominator so
The exponent is unhappy in the denominator so
move to the numerator and it becomes positive.
Let's look at some more challenging examples
Remember to work slowly and meticulously. You will need to memorize the rules for exponents. A shortened version:
Multiply → Add exponents
Divide → Subtract exponents
Power to a power → Multiply exponents
Negative → Change "floors"
To link to this Positive and Negative Integer Exponents page, copy the following code to your site: