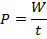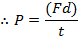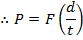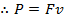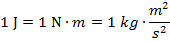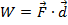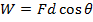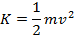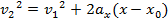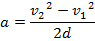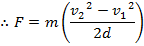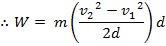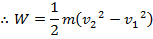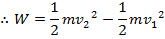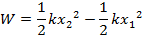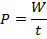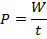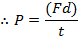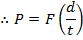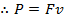Work, Energy, and Power

Work

Work has a specific definition in physics. Work is done when a force is exerted on an object, and the object moves from one place to another. Work is the result of a force, acting over a certain distance. This distance is called the displacement of the object. If the force F, and the displacement d, are in the same direction, then the work W is given by the formula,

W = Fd

The work is the product of the force and the displacement. In SI (international system) units, the unit of force is the Newton (N), and the unit of distance or displacement is the meter (m). Therefore, the unit of work can be expressed as a Newton-meter, N∙m. This is also known as a Joule, J. The Newton is a compound unit, and so a Joule is also equal to,



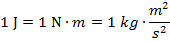
The equation W = Fd depends on the force and the displacement being in the same direction. There are many situations in which their directions are different, for example, a person pushing on a box close to the ground. A component of the force the person applies is directed down, even though the resulting direction of the box is forward. In a case like this, only the component of the force that is along the path of the box's displacement contributes to the work done. If we treat the force and the displacement as vectors, the work can be found by using the dot product (also known as the scalar product). The work is equal to,





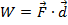
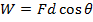
In this formula, θ is the angle between the force and displacement vectors, and F and d are the magnitudes of the vectors.

Energy

The kinetic energy (K) of an object is equal to the amount of work that is required to accelerate the object from rest to a certain velocity, v. This relationship between kinetic energy and work is called the work-energy theorem. The kinetic energy of an object is a scalar value, meaning it does not depend on the direction the object moves in. The value of kinetic energy is always positive or zero. The unit of kinetic energy is the same as the unit of work, the Joule (J).

The kinetic energy of an object can be related to its mass and velocity with the formula,



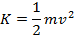
This formula for kinetic energy can be found from the equation for work, if the force is in the same direction as the object's displacement. This formula depends on the kinematic formula,



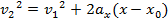
The change in position, (x - x₀), is equal to the displacement magnitude, d. The formula can be rearranged to isolate for the acceleration, a,



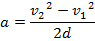
Force is equal to the mass of an object multiplied by its acceleration, so the force is,

F = ma



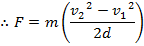
This formula for force can be substituted in to the formula for work,

W = Fd







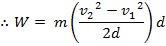
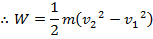
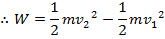
Therefore, the work done by the force on an object is equal to the change in the object's kinetic energy,

W = K₂ - K₁

W = ΔK

In this formula, the Greek uppercase letter Δ ("delta") is used to mean "the change in".

Work can be used to understand the energy of many objects that experience forces. One example is the work required to stretch a spring. If the magnitude of the displacement of the object is labeled x, and this represents the displacement away from an equilibrium position x = 0, then the force required to pull the object on the spring to a position x is,

F = kx

The constant k in this equation is the spring constant, which is different for every spring. The spring constant has units Newtons per meter, N/m. The work required to pull the spring from any starting position x₁ to a final position x₂ is,



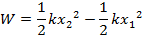Power

Power is a rate of doing work. It is a measure of how quickly work is done. For a quantity of work W that is done in an amount of time t, the power done is,



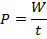
The unit for power is the Watt (W), which is equal to a Joule per second,

1 W=1 J/s

Power can also be expressed in as force F times velocity v. Since work is given by force times distance, W = Fd, and velocity is distance divided by time, v = d/t, then power is,