force
In simple terms, a force is a push or pull. In physics, it has a more specific definition. A force is a measure of the interactions between objects. force is a vector quantity, and so it has both magnitude and direction. The unit of force is defined in terms of the units of mass and acceleration. In SI units, the unit of force is the Newton (N), which is defined as,
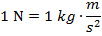
Many forces are the result of direct contact, for example, a person pushing a rock, or pulling a rope that is attached to an object. There are also long-range forces that act on objects that are separated. Examples of forces that act at a distance are gravity, and electromagnetism.
When a number of forces act on an object, the overall effect on the object is equal to the vector sum of the forces. If forces
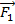
,
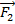
, and so on all act on the object, then the total force (the net force)
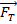
on the object is,
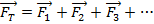
This means that the effect on the motion of the object is the same as if a single force is acting on it. This is called the superposition of forces.
Newton's First Law
Sir Isaac Newton (1643 - 1727) wrote a set of laws of motion that describe how objects are affected by forces. The first of these laws relates to the superposition of forces. The net force on an object is the sum of the forces that act on it (as written above),
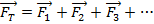
This can also be written in summation notation,
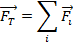
In this notation, the Greek uppercase letter Σ ("sigma") is used to mean "the sum of" all forces, and i is an index to identify each force in the sum.
The net force on an object is zero if all of these forces balance, and so the sum of forces is zero,
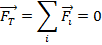
If the net force is zero, then Newton's first law states that the object is in equilibrium. This means that the object is not accelerating or decelerating, though it does not mean that object can't be in motion. If the net force on an object is zero, it can move with a constant velocity. If the object is initially at rest, then it will remain at rest. If it is initially in motion, then it will continue to move at the same velocity.
Newton's first law states that when the vector sum of all forces acting on an object (the net force) is zero, the object is in equilibrium. If the object is initially at rest, it remains at rest. If it is initially in motion, it continues to move with constant velocity.
Newton's Second Law
Newton's second law defines how force is related to the mass of an object. If the net force on an object is not zero, then there is a constant force that causes the acceleration of the object. The relationship between the net force and the acceleration is the mass. The net force is equal to the mass of the object multiplied by the acceleration of the object. The net force and the acceleration are both vectors, and the mass is a scalar value that relates them,
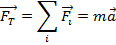
The unit of mass is the kilogram (kg), and the unit of acceleration is m/s
2. This law is often written in terms of the magnitudes of the force and acceleration,
F = ma
Newton's second law states that the vector sum of all forces acting on an object is equal to the mass of the object multiplied by its acceleration (F = ma).
Newton's Third Law
Newton's third law can be stated briefly as, "action is equal to reaction". Any force that acts on an object is the result of an interaction with another object, and each object exerts a force on the other. The forces that act on these objects have equal magnitudes, and opposite directions. For example, if a person kicks a ball, there is a force exerted from the person's foot on the ball, but there is a force of equal magnitude that acts on the person's foot in the opposite direction. This is true whether the forces are the result of direct contact, or whether they are long-range forces.
The third law can be stated as follows. If there are two objects called A and B, and there is a force

that is applied by object A on object B, then there is also a force

that is applied by object B on object A. These forces are equal in magnitude, and opposite in direction,
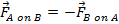
Another way to state Newton's third law is that "for every action force, there is an equal and opposite reaction force". All forces between objects therefore come in action-reaction pairs. It is important to note that each force in the action-reaction pair acts on only one of the two objects. The action and reaction forces never act on the same object.
Newton's Laws, Summary
1) An object is in equilibrium if the net force on it is zero. If an object in equilibrium is initially at rest, it will remain at rest. If it is initially in motion at a constant velocity, it will remain at that velocity.
2) The net force acting on an object is equal to the mass of the object multiplied by its acceleration (F = ma).
3) When two objects interact, they exert forces on each other that are equal in magnitude, and opposite in direction.
Free-Body Diagrams
Free-body diagrams are very useful for solving physics problems that involve Newton's laws. A free-body diagram shows all of the forces that act on a single object. This statement is important, especially regarding the action and reaction force pairs that are related to Newton's third law.
Take, for example, the forces acting on an elevator when it is at a certain floor in a building. In this case, there is the force of gravity, directed downward, and a tension force from the cable that holds it up. The sum of these two forces must be zero, if the elevator is at rest, according to Newton's first law. The free-body diagram for the elevator is below.

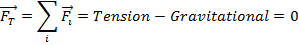
When drawing a free-body diagram, it is important to define the directions of the principal axes. A small drawing indicating which directions are positive in the x and y axes is included.
For the elevator to begin moving, there must be an acceleration. For the elevator to move upward, a motor must increase the tension force on the cable that supports the elevator. In this case, the sum of the forces is equal to the mass times the acceleration of the elevator, according to Newton's second law.

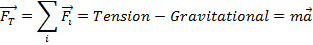
It is important to note that the right-hand side of the equation,
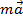
, does not appear in the free-body diagram as a force. It is the sum of all of the forces that are shown. It can sometimes be helpful to draw the direction of the resulting acceleration, but this must be shown as a separate vector, as it appears in the above figure.
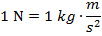
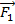 ,
, 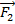 , and so on all act on the object, then the total force (the net force)
, and so on all act on the object, then the total force (the net force) 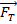 on the object is,
on the object is,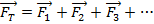
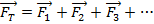
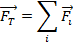
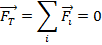
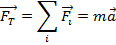
 that is applied by object A on object B, then there is also a force
that is applied by object A on object B, then there is also a force  that is applied by object B on object A. These forces are equal in magnitude, and opposite in direction,
that is applied by object B on object A. These forces are equal in magnitude, and opposite in direction,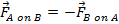

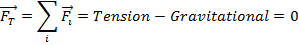

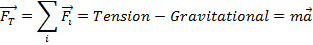
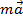 , does not appear in the free-body diagram as a force. It is the sum of all of the forces that are shown. It can sometimes be helpful to draw the direction of the resulting acceleration, but this must be shown as a separate vector, as it appears in the above figure.
, does not appear in the free-body diagram as a force. It is the sum of all of the forces that are shown. It can sometimes be helpful to draw the direction of the resulting acceleration, but this must be shown as a separate vector, as it appears in the above figure.