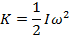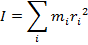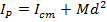Rotational Kinetic Energy
When an object is rotating, every part of that object away from the rotation axis is in motion. Since the object has mass, and every part has a velocity, then each part of the object must have kinetic energy.
If we think of all of the individual particles in a rotating object, the magnitude of the linear velocity for each particle will depend on the angular velocity, and the distance between the particle and the axis. This is expressed with a formula from a previous section,
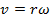
We assume that the object is rigid, meaning that the particles within the object don't move relative to each other. This means that every particle in the object has the same angular velocity at any given instant.
The kinetic energy of a particle depends on its mass and velocity, according to the formula from a previous section,
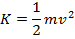
If we assign the particle the mass m, the linear velocity formula above can be substituted in to find the kinetic energy of a particle in the rotating object,
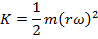
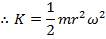
This is the kinetic energy for only one particle within the rotating object. The total kinetic energy can be found by summing over all of the particles. If the particles are numbered, and the letter i represents the number of an individual particle, then the kinetic energy of a particle is,
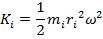
In this formula, K
i is the kinetic energy of the ith particle, m
i is the mass of the ith particle, and r
i is the distance between the rotation axis and the ith particle. The angular velocity
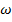
is the same for all particles. The total kinetic energy

of the rotating object is the sum of the individual kinetic energies,
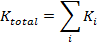
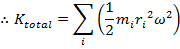
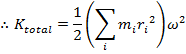
The parts of the expression that depend on the index i of the particle have been gathered inside the brackets. This quantity only depends on the mass and location of the particles within the object. In other words, it depends only on the shape and mass distribution of the object. This quantity is called the
moment of inertia of the object, and it is assigned the label I. The definition of the moment of inertia is,
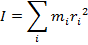
The SI unit of a moment of inertia is the kilogram-meter squared,
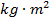
.
Using the moment of inertia, the formula for the kinetic energy of a rotating object becomes,
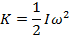
The fact that rotational kinetic energy is defined using the moment of inertia means that it depends on the shape of the object that is rotating. Two rotating objects may have the same mass and angular velocity, but if they have different moments of inertia, they will have different kinetic energies. If the mass of one object is distributed farther from the axis of rotation, the moment of inertia will have a larger value, and therefore it will have more kinetic energy.
Moments of Inertia
The definition of the moment of inertia for any rotating object is,
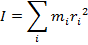
Using this formula requires knowing the mass and location of every particle within the object, and summing over all of them. If the object is simple, like a ball attached to a string being swung in a circle (and the mass of the string is ignored), then the moment of inertia is straightforward to calculate. The moment of inertia is the mass of the ball multiplied by the square of the length of the string. However, for a solid object, with a
continuous distribution of mass, finding the moment of inertia requires knowledge of integral calculus.
For a
uniform object, meaning that the
density of the object's material is the same everywhere there is mass, using integral calculus sometimes yields simple formulas for the moment of inertia. The moments of inertia for some object shapes are given in the following table. The variables that define the shape of the objects are also given.
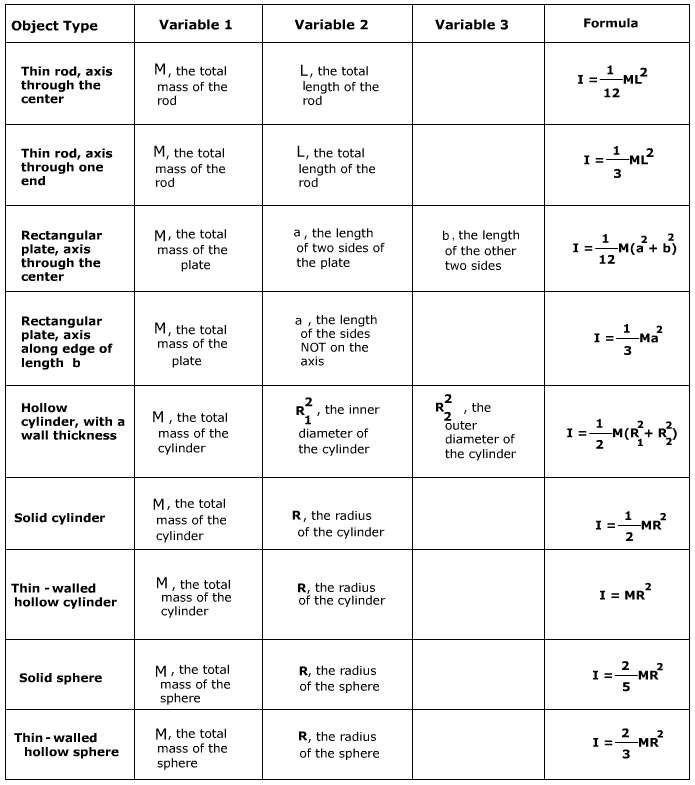
Many physics problems that assume objects are one of these shapes can be solved by choosing the correct formula for the moment of inertia. In these formulas, the word "thin" is used to mean that the thickness can be ignored. Remember also that the moment of inertia is the sum of all of the masses of an object. This means that more complex objects can be created by adding these formulas for the moment of inertia together. For example, a rod with a mass at each end will have a moment of inertia equal to the moment of inertia of the rod, plus the moment of inertia of each mass.
Parallel Axis Theorem
The moment of inertia of an object changes if the axis of rotation is changed. Take for example the first two formulas in the above table. The first formula is for a thin rod with an axis of rotation through its center. The second is for a thin rod with an axis of rotation at one end, and it differs from the first formula.
Given the moment of inertia for an axis through an object's center of mass, it is possible to find the value of the moment of inertia for any other axis that is parallel to the first. This is called the
parallel axis theorem.
We label the moment of inertia for an axis of rotation through an object's center of mass as I
cm, and the moment of inertia around a parallel axis as I
P. If the distance between the two axes is d, then the moment of inertia at the parallel axis is,
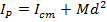
In this formula, M is the total mass of the object.
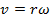
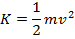
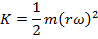
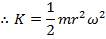
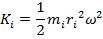
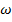 is the same for all particles. The total kinetic energy
is the same for all particles. The total kinetic energy  of the rotating object is the sum of the individual kinetic energies,
of the rotating object is the sum of the individual kinetic energies,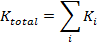
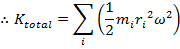
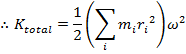
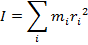
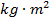 .
.