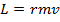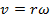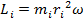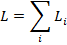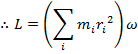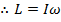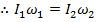Torque
Torque is the result of applying a force to rotate an object around an axis. It is a measure of the tendency of a force to change the rotational motion of an object. In a previous section, angular acceleration was introduced, but the possible sources of this were not discussed. Applying a force to produce a torque is one way that angular acceleration can be applied. The SI unit of torque is the Newton-meter,
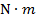
.
Torque depends on an applied force, but it also depends on the distance between the rotation axis and the location that the force is applied. This distance is called either the
lever arm or moment arm. Torque is a vector quantity, but it is important to note that it does not point in the direction of the applied force, or along the moment arm. The torque vector points along the axis of rotation, in one of two directions. This means that the torque vector is always perpendicular to the applied force and the moment arm.
The formula for torque depends on the cross product of two vectors, which was presented in a previous section. The "cross" or "vector" product of two vectors
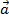
and
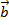
is written
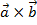
. The result of the cross product is a vector value, equal to the magnitudes of the vectors multiplied by the sine of the angle between them θ, and multiplied by a unit vector that is perpendicular to both
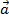
and
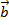
, which is given the label
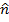
,
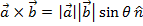
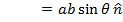
,
The vector
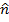
can point in the positive or negative direction, and this direction can be found using the right-hand rule (the direction of your right thumb when curling your fingers from the first vector to the second vector).
The formula for the torque vector is,
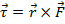
The label used for torque is the Greek letter
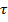
("tau"). The vector
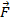
is the applied force, and the vector
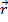
is the vector drawn from the axis of rotation to the location where the force is applied. The magnitude of the vector
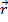
is therefore the moment arm length. The torque vector is equal to,
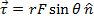
The angle θ is the angle between the moment arm and the force. If this value is 90° (which is equal to π/2 radians), then the force is perpendicular to the moment arm, and the torque is,
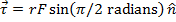
(perpendicular force and moment arm)
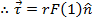
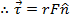
So, when the moment arm and applied force are perpendicular, the sine term is equal to 1, and the magnitude of the torque is,
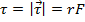
(perpendicular force and moment arm)
The direction of the torque can be found using the right-hand rule, by curling the right hand from the moment arm vector to the force vector, and following the direction of the thumb. For an object that appears to be rotating clockwise, this means that the direction of the torque vector is down. For an object that appears to be rotating counter-clockwise, the torque vector points up.
In general, the tangential component of the applied force (
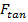
) has a magnitude of,
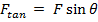
The magnitude of the torque is therefore,
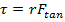
(force with any component perpendicular to the moment arm)
Torque and Angular Acceleration
Imagine an object that is rotating around the z axis. Imagine the particles that compose this object, and imagine a specific particle that has a mass m, and tangential acceleration
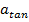
. By Newton's second law the magnitude of the force on the particle is,
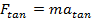
In a previous section, a formula was developed that related the tangential acceleration of a point on a rotating object and the angular acceleration. The tangential acceleration of the particle at this point is equal to,
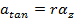
In this formula,
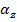
is the angular acceleration of the object, assuming that it rotates around the z axis. The tangential component of the force on the particle is,
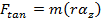
The magnitude of the torque on the particle can be found using this formula for the tangential component of the force,
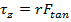
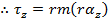
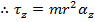
This is the torque on an individual particle at a distance r from the rotation axis (the z axis, in this case). We can sum over all of the particles if they are numbered, and the letter i represents the number of an individual particle. The magnitude of the torque on the particle with index number i is
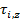
, the particle's mass is m
i, and it is at distance r
i from the axis. The magnitude of the torque on the particle is,
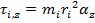
The total magnitude of the torque around the z axis for the rotating object is the sum of all of the individual torques,
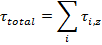
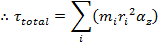
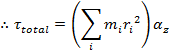
The parts of the expression that depend on the index i of the particle have been gathered inside the brackets. In a previous section, this was identified as the moment of inertia of the object, which is assigned the label I. The definition of the moment of inertia is,
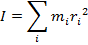
The SI unit of a moment of inertia is the kilogram-meter squared,
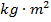
.
Expressed using the moment of inertia, the total magnitude of the torque on an object becomes,
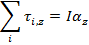
This formula bears a resemblance to the formula for Newton's second law, as shown in a previous section,
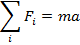
The torque formula can be referred to as the rotational analog of Newton's second law.
Angular Momentum
The concept of linear momentum was introduced in a previous section. Momentum also has a rotational analog. The discussion of torque showed that it is the result of applying a force at a distance from the axis of rotation. The
angular momentum of a rotating object is labeled
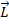
, and it is the result of linear momentum at a distance from the axis of rotation. The formula for angular momentum is,
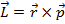
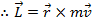
The SI units of angular momentum are
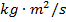
. The vector
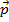
is the linear momentum, which can also be written in terms of the linear velocity,
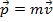
. The vector
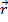
is the vector drawn from the axis of rotation to the location of the linear momentum vector.
The angular momentum vector is equal to,
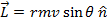
The angle θ is the angle between the moment arm and the linear momentum. If this value is 90° (which is equal to π/2 radians), then the linear momentum is perpendicular to the moment arm, and the angular momentum is,
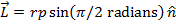
(perpendicular linear momentum and moment arm)
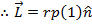
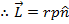
So, when the moment arm and linear momentum are perpendicular, the sine term is equal to 1, and the magnitude of the angular momentum is,
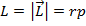
(perpendicular linear momentum and moment arm)
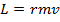
The direction of the angular momentum can be found using the right-hand rule, by curling the right hand from the moment arm vector to the linear momentum (or velocity) vector, and following the direction of the thumb.
As with torque, it is possible to express angular momentum in terms of the moment of inertia of the rotating object. This depends on the relation between linear and angular velocity presented in a previous section. For a point on an object rotating around the z axis, the linear velocity is,
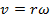
A particle within the rotating object with index number i has angular momentum of magnitude,
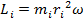
The total magnitude of the angular momentum around the z axis is the sum of the individual angular momenta,
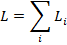
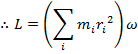
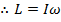
In this formula, I is the moment of inertia around the z axis.
Conservation of Angular Momentum
In a previous section, we saw conservation laws for energy and linear momentum. Another universal conservation law is the
conservation of angular momentum. When there is no external torque acting on a system, the total angular momentum of the system is conserved.
This is useful when a system that can change its moment of inertia is considered, for example, a spinning figure skater. When the skater brings her arms in close during her spin, or extends them out, her moment of inertia changes. If the friction on her skate is ignored, she has no external torques acting on her during her spin. For angular momentum to be conserved when her moment of inertia changes, her angular velocity must also change.
For conditions, labeled 1 and 2, the angular momentum remains constant, and so the product of the moment of inertia and angular velocity remains constant,
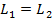
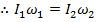
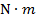 .
.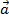 and
and 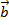 is written
is written 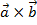 . The result of the cross product is a vector value, equal to the magnitudes of the vectors multiplied by the sine of the angle between them θ, and multiplied by a unit vector that is perpendicular to both
. The result of the cross product is a vector value, equal to the magnitudes of the vectors multiplied by the sine of the angle between them θ, and multiplied by a unit vector that is perpendicular to both 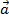 and
and 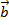 , which is given the label
, which is given the label 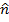 ,
,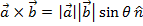
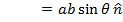 ,
,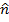 can point in the positive or negative direction, and this direction can be found using the right-hand rule (the direction of your right thumb when curling your fingers from the first vector to the second vector).
can point in the positive or negative direction, and this direction can be found using the right-hand rule (the direction of your right thumb when curling your fingers from the first vector to the second vector).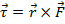
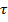 ("tau"). The vector
("tau"). The vector 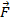 is the applied force, and the vector
is the applied force, and the vector 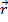 is the vector drawn from the axis of rotation to the location where the force is applied. The magnitude of the vector
is the vector drawn from the axis of rotation to the location where the force is applied. The magnitude of the vector 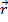 is therefore the moment arm length. The torque vector is equal to,
is therefore the moment arm length. The torque vector is equal to,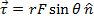
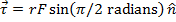 (perpendicular force and moment arm)
(perpendicular force and moment arm)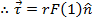
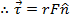
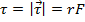 (perpendicular force and moment arm)
(perpendicular force and moment arm)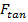 ) has a magnitude of,
) has a magnitude of,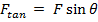
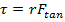 (force with any component perpendicular to the moment arm)
(force with any component perpendicular to the moment arm)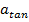 . By Newton's second law the magnitude of the force on the particle is,
. By Newton's second law the magnitude of the force on the particle is,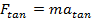
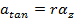
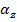 is the angular acceleration of the object, assuming that it rotates around the z axis. The tangential component of the force on the particle is,
is the angular acceleration of the object, assuming that it rotates around the z axis. The tangential component of the force on the particle is,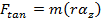
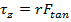
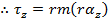
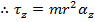
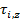 , the particle's mass is mi, and it is at distance ri from the axis. The magnitude of the torque on the particle is,
, the particle's mass is mi, and it is at distance ri from the axis. The magnitude of the torque on the particle is,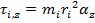
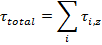
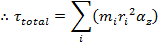
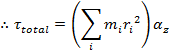
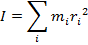
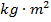 .
.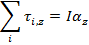
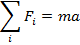
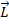 , and it is the result of linear momentum at a distance from the axis of rotation. The formula for angular momentum is,
, and it is the result of linear momentum at a distance from the axis of rotation. The formula for angular momentum is,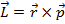
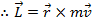
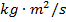 . The vector
. The vector 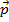 is the linear momentum, which can also be written in terms of the linear velocity,
is the linear momentum, which can also be written in terms of the linear velocity, 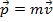 . The vector
. The vector 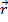 is the vector drawn from the axis of rotation to the location of the linear momentum vector.
is the vector drawn from the axis of rotation to the location of the linear momentum vector.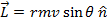
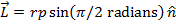 (perpendicular linear momentum and moment arm)
(perpendicular linear momentum and moment arm)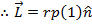
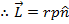
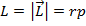 (perpendicular linear momentum and moment arm)
(perpendicular linear momentum and moment arm)