Complementary or Supplementary
To determine whether an angle pair is complementary or supplementary you have to recall the definition of complementary and supplementary.
Complementary - two angles whose sum is 90°
Supplementary - two angles whose sum is 180°
Example 1
Identify a pair of complementary and supplementary angles.
m
1 = 40°
m2 = 140°
m3 = 50°
m1 + m 3 = 90° therefore 1 and 3 are complementary.
m 1 + m 2 = 180° therefore 1 and 2 are supplementary.
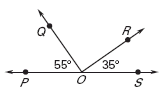
Example 2: Determine if angles POQ and ROS are complementary or supplementary.
m POQ is 55°
mROS is 35°
55° + 35° = 90° Therefore the angles are complementary.
Example 3: Identify a pair of complementary and a pair of supplementary angles.
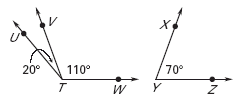
mUTV is 20°
mVTW is 110°
mXYZ is 70°
mUTV + m XYZ = 20° + 70° = 90°
UTV and XYZ are complementary
mVTW + m XYZ = 110° + 70° = 180° VTW and XYZ are supplementary
Example 4: Identify a pair of complementary and a pair of supplementary angles.
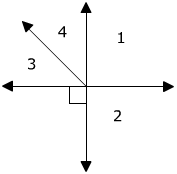
3 + 4 = 90°
1 + 2 = 90° + 90° = 180°
Quick Summary:
There are two methods to determining if an angle pair is complementary: (1) if you are looking at a diagram you will be looking for two adjacent angles that form a right angle.
(2) you can add the measure of any two angles and see if their sum is 90°.
There are two methods to determining if an angle pair is supplementary: (1) if you are looking at a diagram you will be looking for two adjacent angles that form a linear pair.
(2) you can add the measure of any two angles and see if their sum is 180°.
Complementary - two angles whose sum is 90°
Supplementary - two angles whose sum is 180°
Example 1
Identify a pair of complementary and supplementary angles.
m
1 = 40°m
2 = 140°m
3 = 50°m
1 + m 3 = 90° therefore 1 and 3 are complementary.m 1 + m 2 = 180° therefore 1 and 2 are supplementary.
Example 2: Determine if angles POQ and ROS are complementary or supplementary.
m POQ is 55° m
ROS is 35°
55° + 35° = 90° Therefore the angles are complementary.
Example 3: Identify a pair of complementary and a pair of supplementary angles.
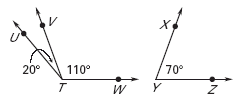
m
UTV is 20°m
VTW is 110°m
XYZ is 70°m
UTV + m XYZ = 20° + 70° = 90°
UTV and XYZ are complementarym
VTW + m XYZ = 110° + 70° = 180° VTW and XYZ are supplementaryExample 4: Identify a pair of complementary and a pair of supplementary angles.
-
3 and 4 form a right angle. A right angle is 90° therefore they are complementary.
3 + 4 = 90°-
1 and 2 are a linear pair which means they are supplementary. m 1 = 90° and m 2 = 90°
1 + 2 = 90° + 90° = 180°Quick Summary:
There are two methods to determining if an angle pair is complementary: (1) if you are looking at a diagram you will be looking for two adjacent angles that form a right angle.
(2) you can add the measure of any two angles and see if their sum is 90°.
There are two methods to determining if an angle pair is supplementary: (1) if you are looking at a diagram you will be looking for two adjacent angles that form a linear pair.
(2) you can add the measure of any two angles and see if their sum is 180°.
|
Related Links: Math Geometry Topics Polygons Supplementary Angles |
To link to this Complementary or Supplementary page, copy the following code to your site: