Supplementary Angles
The definition of supplementary is two angles whose sum is 180° are supplementary. The angles can be either adjacent (share a common side and a common vertex and are side-by-side) or non-adjacent.
Example 1. Given m 1 = 45° and m 2=135° determine if the two angles are supplementary.
45° + 135° = 180° therefore the angles are supplementary.
We will use the following facts to help us determine if two angles are supplementary.
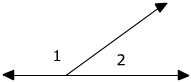
Example 2: the angles form a line (linear pair) therefore they are supplementary
Example 3: the angles can be non-adjacent as long as their sum is 180°
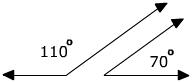
110°+ 70° = 180° The sum is 180° therefore they are supplementary.
Example 4:
 1 and
1 and  2 form a linear pair so m
2 form a linear pair so m  1 + m
1 + m  2 = 180° therefore the angles are supplementary.
2 = 180° therefore the angles are supplementary.

How many other linear pairs can you see in the diagram?



m 2 + m
2 + m  3 = 180°
m
3 = 180°
m  3 + m
3 + m  4 = 180°
m
4 = 180°
m  1 + m
1 + m  4 = 180°
4 = 180°
Remember that linear pairs are supplementary and that 2 intersecting lines will form 4 pairs of supplementary angles.
Geometry & Algebra: find the value of x the find the m ABD and m
ABD and m  DBC.
DBC.
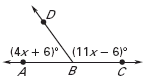
Write an equation (4x +6) ° + (11x - 6)°= 180°
Identify like terms (4x +6) ° + (11x - 6)°= 180°
Combine like terms 4x + 11x +6 - 6 = 180°
15x + 0 = 180°
The zero is unnecessary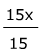 =
=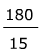
Divide both sides by 15
x = 12
m ABD = 4x + 6 = 4(12)+6 = 54°
ABD = 4x + 6 = 4(12)+6 = 54°
m DBC = 11x - 6 = 11(12) -6 = 126°
DBC = 11x - 6 = 11(12) -6 = 126°
check your answer 54° + 126° = 180°
Sum it up: Supplementary angles are two angles whose sum is 180°. A linear pair (two angles that form a line) will always be supplementary. The two angles can be adjacent or non-adjacent.
Example 1. Given m 1 = 45° and m 2=135° determine if the two angles are supplementary.
45° + 135° = 180° therefore the angles are supplementary.
We will use the following facts to help us determine if two angles are supplementary.
- A linear pair is two angles that are adjacent and form a line.
- The angle measure of a line is 180°
- If two angles form a linear pair then they are supplementary.
Example 2: the angles form a line (linear pair) therefore they are supplementary

Example 3: the angles can be non-adjacent as long as their sum is 180°

110°+ 70° = 180° The sum is 180° therefore they are supplementary.
Example 4:
 1 and
1 and  2 form a linear pair so m
2 form a linear pair so m  1 + m
1 + m  2 = 180° therefore the angles are supplementary.
2 = 180° therefore the angles are supplementary.
How many other linear pairs can you see in the diagram?



m
 2 + m
2 + m  3 = 180°
m
3 = 180°
m  3 + m
3 + m  4 = 180°
m
4 = 180°
m  1 + m
1 + m  4 = 180°
4 = 180°Remember that linear pairs are supplementary and that 2 intersecting lines will form 4 pairs of supplementary angles.
Geometry & Algebra: find the value of x the find the m
 ABD and m
ABD and m  DBC.
DBC.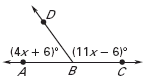
Write an equation (4x +6) ° + (11x - 6)°= 180°
Identify like terms (4x +6) ° + (11x - 6)°= 180°
Combine like terms 4x + 11x +6 - 6 = 180°
15x + 0 = 180°
The zero is unnecessary
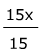 =
=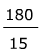
Divide both sides by 15
x = 12
m
 ABD = 4x + 6 = 4(12)+6 = 54°
ABD = 4x + 6 = 4(12)+6 = 54°m
 DBC = 11x - 6 = 11(12) -6 = 126°
DBC = 11x - 6 = 11(12) -6 = 126°check your answer 54° + 126° = 180°
Sum it up: Supplementary angles are two angles whose sum is 180°. A linear pair (two angles that form a line) will always be supplementary. The two angles can be adjacent or non-adjacent.
|
Related Links: Math Geometry Topics Complementary Angles Complementary or Supplementary |
To link to this Supplementary Angles page, copy the following code to your site:
