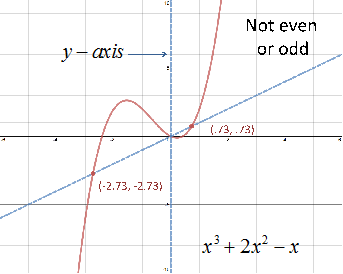Home > Math > Calculus > Even and Odd Functions

Even and Odd Functions

Some graphs exhibit symmetry. Graphs that have symmetry with respect to the y-axis are called even functions. Graphs the have symmetry with respect to the origin are called odd functions.

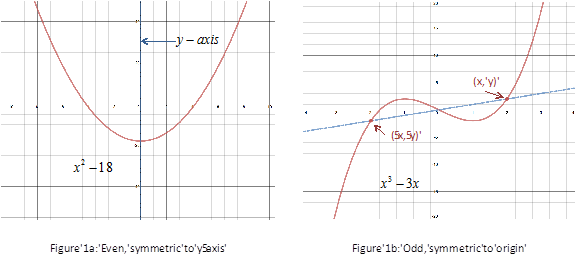
Look at the graphs of the two functions f(x) = x2 - 18 and g(x) = x3 - 3x. The function f(x) = x2 - 18 is symmetric with respect to the y-axis and is thus an even function. The function g(x) = x3 - 3x is symmetric about the origin and is thus an odd function.



Stated another way, functions are even if changing x to -x does not change The value of the function.

EVEN FUNCTION:


     f(x) = x2 - 18f(-x) = (-x)2 - 18 = x2 - 18


Since f(-x) = f(x) the function is even.



Functions are odd if changing x to -x negates the value of the function.

ODD FUNCTION:


     f(x) = x3 - 3xf(-x) = (-x)3 - 3(-x) = -x3 + 3x = -(x3 - 3x)


Since f(-x) = -f(x) the function is odd.



A function can be even, odd or neither even nor odd. To determine if a function has even or odd symmetry use the following guidelines.

GUIDELINES TO DETERMINE EVEN OR ODD SYMMETRY


1. Replace the f(x) with f(-x) and simplify the function.

2. Compare the results of step 1 to f(x) and -f(x).

3. Determine if the function is even, odd or neither

a. If f(-x) results in the same value as f(x), the function is even.

b. If f(-x) results in the same value as -f(x), the function is odd.

c. If f(-x) did not result in step a or b, the function is neither even nor odd.


Let's look at a couple examples.

Example 1: Determine if the function f(x) = x6 + 4x2 - 1 is even, odd or neither then graph the function and describe the symmetry.

Step 1: Replace f(x) with f(-x) and simplify the function.

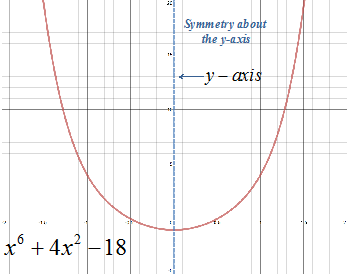
Original function:


f(x) = x6 + 4x2 - 1


Substitute x with -x:


f(-x) = (-x)6 + 4(-x)2 - 1


Simplify:


f(-x) = x6 + 4x2 - 1

Step 2: Compare f(-x) to f(x) and -f(x).

f(-x) = x6 + 4x2 - 1


f(x) = x6 + 4x2 - 1


Compare f(-x) to f(x):


x 6 +4 x 2 −1= x 6 +4 x 2 −1


Since f(-x) to f(x) there is no need to compare f(-x) to -f(x) because the function cannot be both.

Step 3: Determine if the function is even, odd, or neither.

Since f(-x) = f(x) the function is even and has symmetry about the y-axis.

Step 4: Graph the function


Example 2: Determine if the function f(x) = x3 + 2x2 - x is even, odd or neither then graph the function and descried the symmetry.

Step 1: Replace f(x) with f(-x) and simplify the function.

Original function:


f(x) = x3 + 2x2 - x


Substitute x with -x:


f(-x) = (-x)3 + 2(-x)2 - (-x)


Simplify:


f(-x) = -x3 + 2x2 + x

Step 2: Compare f(-x) to f(x) and -f(x).

f(-x) = -(x3 - 2x2 - x)


f(x) = x3 + 2x2 - x


-f(x) = -(x3 + 2x2 - x)


Compare f(-x) to f(x):


−( x 3 −2 x 2 −x)≠ x 3 +2 x 2 −x


Compare f(-x) to -f(x):


−( x 3 −2 x 2 −x)≠−( x 3 +2 x 2 −x )

Step 3: Determine if the function is even, odd, or neither.

Since f(-x) does not equal f(x) or -f(x) the function is neither even nor odd.

Step 4: Graph the function






Related Links:
Math
algebra
Function Transformations
Rolle's Theorem
Calculus Topics


To link to this Even and Odd Functions page, copy the following code to your site: