Solving Inequalities with Multiplication/Division
|
Solving inequalities is very similar to solving equations, but sometimes you have to reverse the symbol. We discussed in the last lesson that if you want to switch sides of the equation, you must reverse the symbol. There is one other time. You must reverse the inequality symbol when you multiply or divide both sides of the equation by a negative number. Did you catch the two parts to that?
1) It must be multiplication or division (not addition or subtraction) 2) The number being multiplied or divided must be negative. Other than that, everything is the same. To move something multiplied or divided, do the reverse operation to both sides. Here's a couple examples:
1) -3x≤12The -3 is being multiplied, so we must divide both sides by -3. Notice 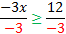 that since we are dividing both sides by a negative number, we mustx≥-4 reverse the inequality symbol. 2) 5x>-10The 5 is being multiplied, so we must divide both sides by 5. Notice 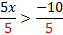 that since we are dividing both sides by a positive number (5), we do not reverse the symbol. It doesn't matter that the 10 is negative.x>-2 The only number that matters is the one that is being multiplied or divided. Practice:Solve the following equations. 1) 7x>10 2) -2y≥8 3) 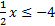 4) -3a<-12 5) 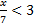 Answers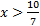: 1)  2)
y≤-43) x≤-84) a>4 5) x<21 |