src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML">
When considering triangles there are several important facts that will assist in answering the majority of the GMAT questions related to triangles.
1. Triangles can be classified in the following ways:
a. Right - has at least 1 right (90°) angle
b. Scalene - each side and each angle have different measures
c. Obtuse - has one angle that is greater than 90°
d. Acute - all three angles are less than 90°
e. Equilateral - every angle is equal (60°) and every side is equal
f. Isosceles - two angles and two sides are equal
2. The measure of all interior angles in a triangle equal to 180°
3. The sum of the measure of any two sides must be greater than the measure of the third side.
4. The longest side (hypotenuse) of a triangle is always located opposite the angle with the largest measure.
5. The exterior angle theorem states that ∠A + ∠B = ∠DCB
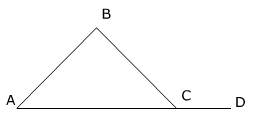
6. Triangles can be considered similar (have the same ratios) in the following situations:
a. Angle Angle Angle (AAA) - the corresponding 3 angles of each triangle have the same measurement.
b. Side Angle Side (SAS) - the corresponding angle of the triangles have the same measure and the two sides that enclose that angle have the same measure in both triangles.
c. Side Side Side (SSS) - the corresponding side of the triangles have the same ratio
7. Triangles can be considered congruent in the following situations:
a. Side Angle Side (SAS) - the corresponding angle of the triangles have the same measure and the two sides that enclose that angle have the same measure in both triangles.
b. Side Side Side (SSS) - the corresponding side of the triangles have the same measure
c. Angle Side Angle (ASA) - two pairs of corresponding angles are equal and the side enclosed between them is congruent.
8. Area of a triangle is A = 1/2 base * height
9. Pythagorean Theorem can be used to find the measure of the side of a right triangle with sides a, b, and c where c is the hypotenuse.
a2 + b2 = c2
10. Two types of special triangles are the:
a. 30-60-90 triangle where the sides are in the ratio 1,2, and
b. 45-45-90 triangle where the sides are in the ratio 1,1, and
|