Sine is a trigonometric ratio comparing two sides of a right triangle. Sine is usually shortened to sin but is pronounced sine. This function can be used to determine the length of a side of a triangle when given at least one side of the triangle and one of the acute angles.

Quick Review: the three main trig ratios are sine, cosine and tangent. They can be memorized using SOH CAH TAH What does this mean? It means that sine is the ratio of the opposite side divided by the hypotenuse.

Sinθ =

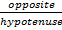
Let's look at an example at how sine can be used to find the length of the opposite side.



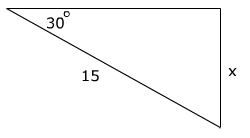
To find x write an equation using the sine ratio and then solve for x

Sine 30° = 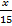use the multiplication property to isolate x

(15) sin 30 = 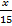(15)You will need to use a calculator to find the value of sin 30°

(15) (.5) = x make sure your calculator is in degree mode by verifying that Sin 30 = .5

7.5 = x the side length represented by x has a length of 7.5

Now let's look at how Sine can be used to find the length of the hypotenuse.



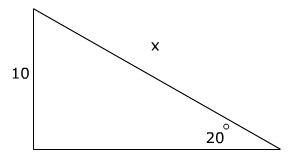
To find x write an equation using the sine ratio and then solve for x

Sine 20° = 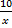use the multiplication property to eliminate the fraction

(x) sin 20° = 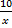(x)You will need to use a calculator to find the value of sin 20°. Round to 4 decimal places

Make sure your calculator is in degree mode by verifying that (x) (.3420) = 10      Sin 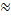20 .3420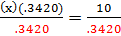

Divide both sides by .3420 to isolate x

x = 29.2398 Round your answer to the nearest tenth

x = 29.2    the length of the hypotenuse is 29.2

The trig ratios have many real world and practical applications in fields such as aviation, architecture, surveying. Using the trigonometric ratios, such as sine, allows for the measurement of things that cannot be determined using typical measurement tools.

Related Links: Math Trigonometry The Tangent Function in Right Triangles Graphing the Cosine Function