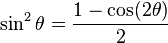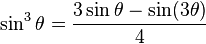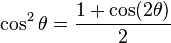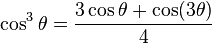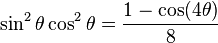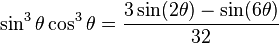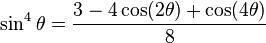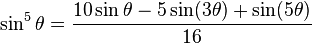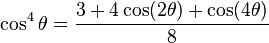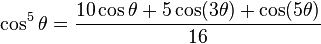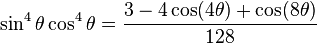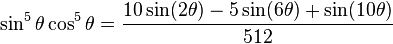The purpose of the power reduction formulas is to write an equivalent expression without an exponent. They are used to simplify calculations and are derived through the use of the double angle and half angle formulas and the Pythagorean identity.

Squares	Cubes
Fourths	Fifths

Example: Find

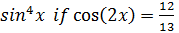
Step 1: write sin⁴ x as a squared term

sin⁴ x = (sin²x)²

Step 2: use the squared power reduction rule for sine

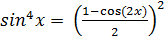
Step 3: substitute using

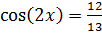
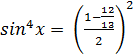
Step 4: Simplify

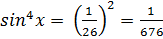
Although the formula for the fourth power could have been used, it is much simpler to write the fourth power in terms of a squared power so that a double angle or half angle formula does not have to be used as well. Power-reducing formulas become very handy in calculus by allowing you to get rid of exponents in trigonometric functions in order to solve for an angle's measure.

Related Links: Math Trigonometry Product to Sum and Sum to Product Formulas Double Angle Identities