Each of the trigonometric functions sine, cosine, tangent, secant, cosecant and cotangent has an inverse (with a restricted domain). The inverse is used to obtain the measure of an angle using the ratios from basic right triangle trigonometry. The inverse of sine is denoted as Arcsine or on a calculator it will appear as asin or sin^-1. Note: this does NOT mean sine raised to the negative one power.

Let's look at an example of how to use the inverse sine function to find the measure of an angle in a right triangle. (triangle not drawn to scale)



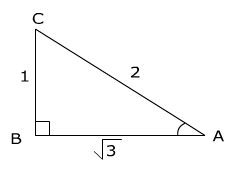
To find the measure in degrees of angle A using the sine inverse, recall that



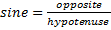
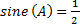
Use a scientific calculator 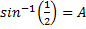*Make sure your calculator is in degree mode

30° = A

Let's look at an application problem.

An airplane is 6000 feet above ground. It is 10,000 feet from the runway. At what angle must the plane descend to land on the target runway?

Begin by creating a sketch that will organize the data and show a right triangle.

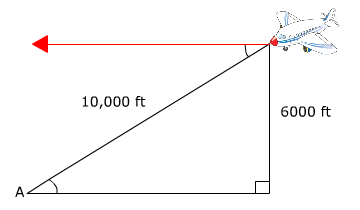   *Alternate interior angles are congruent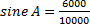



Use a scientific calculator 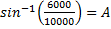   *Make sure your calculator is in degree mode

36.9° A rounded to the nearest tenth

If it is understood how to use the basic right triangle trigonometric ratios, then the inverse can be used to find a missing angle measure in any right triangle. Sine, cosine, secant, tangent, cosecant and cotangent are all functions however, the inverses are only a function when given a restricted domain.

Related Links: Math Trigonometry Inverse Tangent Function (Arctangent) Graphing a Sine Function