The half angle formulas can be used to find the exact values of unknown trig functions. For example, you might not know the sine of 75 degrees, but by using the half angle formula for sine, you can figure it out based on the known value of sin(150) = 1/2.

They are also useful for certain integration problems where a double or half angle formula may make things much simpler to solve when finding exact answers.

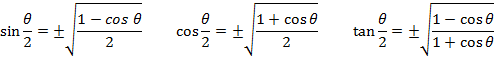
Example: find the sine of 75 degrees using a half angle formula

Sin 75 =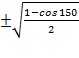

=

=

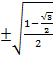
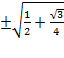
At this point the correct sign has to be decided. 75 degrees is in quadrant I and sine is positive in Quadrant I therefore the final answer will be positive.

Sin 75 =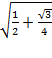

Example: find the cosine of 112.5 degrees using a half angle formula

=

=

=

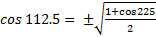
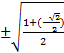
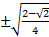
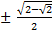
At this point the correct sign has to be decided. 112.5 degrees is in quadrant II and cosine is negative in Quadrant II therefore the final answer will be negative.

Cos 112.5° = -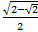

The double and half angle formulas are strategies that are meant to help simplify to an exact answer when feasible. When doing trigonometry there are multiple ways to get a correct answer.

Related Links: Math Trigonometry Even and Odd Trig Functions Power Reduction Formula