Double angle identities can be used to solve certain integration problems where a double formula may make things much simpler to solve. Notice that there are several listings for the double angle for cosine. That's because you can substitute for either of the squared terms using the basic trigonometric identity sin²θ + cos²θ = 1.

cos2 θ = cos2θ - sin2θ sin2 θ = 2sin θ · cosθ cos2θ = 1 - 2 sin2θ 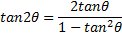cos2θ = 2 cos2θ - 1

Example: If

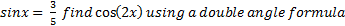
cos2x = 1 - 2 sin² x

Substitute

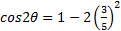
Simplify

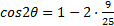
Simplify

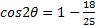
Simplify

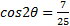
Example: Find all the solutions of 2 cosθ + sin2θ = 0     where

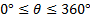
1) Replace sin2θ with 2sin θ · cos θ

2cosθ + 2sin θ · cos θ = 0

2) Factor out the common factor of 2 cosθ

2cos θ (1 + sinθ) = 0

3) Use the zero product rule

2 cos θ = 01 + sinθ = 0

cosθ = 0    sin θ = -1

4) Determine when cos θ = 0 and sin θ = -1

cos θ = 0 when θ is 90°

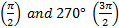
sin θ = -1 when

Therefore the solution set is 90°

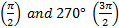
Related Links: Math Trigonometry Half Angle formulas Even and Odd Trig Functions Sum and Difference of Angles Identities