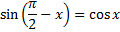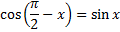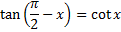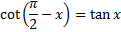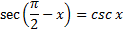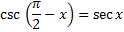Home > Math > Trigonometry > Cofunction Identities

Cofunction Identities

The cofunction identities show the relationship between sine, cosine, tangent, cotangent, secant and cosecant. The value of a trigonometric function of an angle equals the value of the cofunction of the complement. Recall from geometry that a complement is defined as two angles whose sum is 90°.

For example: Given that the the complement of

Radians


Sine and cosine are cofunctions and complements

Tangent and cotangent are cofunctions and complements

Secant and cosecant are cofunctions and complements



Degree


Sine and cosine are cofunctions and complements

sin(90° - x) = cos x

cos(90° - x) = sin x

Tangent and cotangent are cofunctions and complements

tan(90° - x) = cot x

cot(90° - x) = tan x

Secant and cosecant are cofunctions and complements

sec(90° - x) = csc x

csc(90° - x) = sec x



Degree Example:


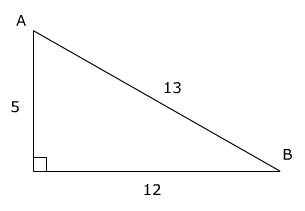
sin A = 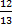cos B =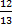

A = 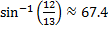B =

cos(90° - A) = sin A

Using substitution:cos(90° - 67.4°) = sin 67.5°

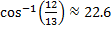
cos(22.6°) = sin(67.5)°


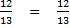
Therefore, the value of cosine B is equal to sine A which is the cofunction and complement of B. The process remains the same whether you are in degree mode or radian mode.

Let's see how this can be applied.

Use the cofunction identities to evaluate the expression without a calculator!

sin2 (23°) + sin2 (67°)

Step 1: Note that 23° + 67° = 90° (complementary)

Step 2: use the cofunction identity and let x = 23°sin(90° - x) = cos x


therefore sin(67°) = cos(23°)


Step 3: use substitution sin2(23°) + cos2(23°)


Step 4: use the Pythagorean identity sin2θ + cos2θ = 1sin2(23°) + cos2(23°) = 1


Therefore, sin2(23°) + sin2(67°) = sin2(23°) + cos2(23°) = 1





Related Links:
Math
Trigonometry
Sum and Difference of Angles Identities
Trigonometric Identities - Reciprocal Identities


To link to this Cofunction Identities page, copy the following code to your site: