Sometimes our equations have more than one step.

Example:3x + 7 = 28

In this case, we have two steps in order to solve for x. We know that there are two steps because there are two numbers to get rid of before the x will be alone.

So, what has happened to the x? x was multiplied by 3 and then 7 was added to it. If we think of these operations as layers, we have to peel the layers back off and "undo" what has been done.

Think about the order of operations. We know that multiplication comes before addition, but when we are trying to undo something, we need to move backwards through the order of operations. So we first undo the adding, but subtracting.

3x + 7 - 7 = 28 - 7

3x = 21

Now we undo the multiplication by dividing.

3x/3 = 21/3

x = 7

Now we can check to ensure that we have solved correctly. Plug the answer back into the original.

3x + 7 = 28

3(7) + 7 = 28

21 + 7 = 28

28 = 28

When we can show that the answer will create a true statement, we know that we solved correctly.

Here is another example:

4x - 9 = 31

4x - 9 + 9 = 31 + 9 The first step is to add 9 to both sides.

4x = 40

4x/4 = 40/4Then we divide both sides by 4.

x = 10

We can check to see if 10 is the answer by plugging it back in and solving.

4x - 9 = 31

4(10) - 9 = 31

40 - 9 = 31

31 = 31 When we can see that the left is also 31, we know that 10 really is the answer.

Here is one more example:

- 11 = 3 There are still two numbers to get rid of in this example.

- 11 + 11 = 3+ 11Start by using addition to undo the subtraction.

= 14Now we are left with a division question.

• 4= 14• 4We can use multiplication to undo the division.

m = 56

Now, check to make sure the answer is correct by plugging it back into the original.

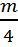- 11 = 3

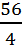- 11 = 3

14 - 11 = 3

3 = 3 Here, we can see that the answer of 56 has made a true statement.


Related Links:
Math
Fractions
Factors