Scientific Notation of Small Numbers
This very small number is just as hard to work with as the very large numbers. So let's take a look at how scientific notation can be used to rewrite this number.
Take a look at the powers of ten:
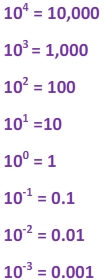
We can see that decimals can be rewritten using negative exponents. For example, if I wanted to write 0.0004, I can think of this as 4 x 0.0001 or we could use an exponent and say that this number is equal to 4 x 10-4. This is an example of scientific notation.
Remember, a number written in scientific notation has two parts:
This first number needs to be greater than or equal to one as well. Nonetheless, lets put the rules to work with some examples.
Examples
1.)0.000003426
Step 1: Move the decimal so that there is only one digit in front of the decimal.
0.000003.426
Step 2: Count the number of moves from the original decimal to the new position.
0.000003.426
 There are 6 moves
There are 6 moves
Step 3: Write the new number as a product with a power of ten.
3.426 x 10-6 The number of moves becomes the exponent.
0.000003.426
Step 2: Count the number of moves from the original decimal to the new position.
0.000003.426
 There are 6 moves
There are 6 movesStep 3: Write the new number as a product with a power of ten.
3.426 x 10-6 The number of moves becomes the exponent.
2.)0.00000000291
Step 1: Move the decimal between the 2 and 9.
0.000000002.91
Step 2:Count the number of moves from one decimal to the other.
0.000000002.91There are 9 moves.

Step 3: Write the new number.
2.91 x 10-9
We can also change a number written in scientific notation back to standard form.
Take a look at how we can use the steps in the opposite order.
0.000000002.91
Step 2:Count the number of moves from one decimal to the other.
0.000000002.91There are 9 moves.

Step 3: Write the new number.
2.91 x 10-9
We can also change a number written in scientific notation back to standard form.
Take a look at how we can use the steps in the opposite order.
Examples:
1.) 5.8 x 10-3
Step 1: Take note of the exponent. The exponent tells us how many times we will move over.
5.8 x 10-3
Step 2: Move the decimal to the left 3 times because the exponent is a negative 3. Place zeros in the empty spots as you move.
.0058
Step 3: Write your final answer.
0.0058
5.8 x 10-3
Step 2: Move the decimal to the left 3 times because the exponent is a negative 3. Place zeros in the empty spots as you move.
.0058
Step 3: Write your final answer.
0.0058
2.) 7 x 10-5
Step 1: The exponent is a negative 5.
Step 2: The decimal is located after the 7. Now it needs to move 5 places to the left.
.00007
Step 3: So the final answer is 0.00007.
Take note that exponent is the number of moves, not the number of zeros!
Step 2: The decimal is located after the 7. Now it needs to move 5 places to the left.
.00007
Step 3: So the final answer is 0.00007.
Take note that exponent is the number of moves, not the number of zeros!
Let's Review:
When faced with a really small number, we can rewrite it so that there are less digits to work with by using powers of ten. The final answer should be a product with a number less than ten (but greater than or equal to one) times a power of ten. When your number in standard form is less than one, but greater than zero, you will have a negative exponent in your scientific notation.
Related Links:
Math
Fractions
Factors
