Equivalent Ratios
Sometimes it is useful to write a ratio in another way. For example, there are 8 cups of strawberries added to a fruit salad for every 16 cups of other fruits. This is an 8:16 ratio of strawberries to other fruits. However, it can also be represented as 1 :2. So if we add one cup of strawberries we can add two cups of other fruits and keep the same mixture in a smaller amount.
We can get equivalent ratios by scaling up or scaling down.
1.)
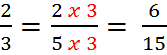This is an example of scaling up by a scale factor of 3. The ratio 2 : 3 is the same as the ratio of 6 : 15.2.)
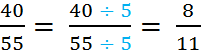This is an example of scaling down by a scale factor of 5. The ratio 8 to 11 is the same as the ratio 40 : 55.3.)
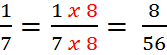Here, we scaled up by a factor of 8 to create two equivalent ratios.We can make a string of equivalent ratios by continuing to scale up or scale down.
1 : 3 = 2 : 6 = 3 : 9 = 4 : 12 = 5 : 15 = 6 : 18 = 7 : 21....
All of these ratios show the same relationship.
Simplifying ratios to the simplest form can be helpful when solving problems that deal with ratios. You can simplify a ratio the same way that you simplify a fraction. This is basically just scaling down until you can no longer scale down anymore.
Examples.
1.) 14 : 18 = 7 : 9
2.) 25 : 500 = 5 : 100 = 1 : 20
3.) 18 : 60 = 9 : 30 = 3 : 10
Let's take a look at how scaling up and scaling down can be helpful with a couple of word problems.
1. At East Ridge Middle School, the ratio of boys to girls is 3 to 2. There are 600 students at the school. How many are boys?
Solution: We have been given the whole. So let's write a ratio that compares the boys to the whole. 3 : 5 is the part-to-whole relationship. Now we can scale up from 5 to 600. 5 x 120 = 600, so 3 x 120 = 360. There are 360 boys at the school.
Solution: We have been given the whole. So let's write a ratio that compares the boys to the whole. 3 : 5 is the part-to-whole relationship. Now we can scale up from 5 to 600. 5 x 120 = 600, so 3 x 120 = 360. There are 360 boys at the school.
2. For every 3 parts of yellow, 5 parts red have been mixed to make a particular shade of orange. If there are 80 gallons of orange made, how many gallons of red were added in?
Solution: The 80 gallons is the whole mixture of paint. So we need a part to whole ratio comparing red to the whole. This would be 5 : 8. Now we can scale up 5 : 8 = 50 : 80. Therefore, 50 gallons of red were used to make the 80 gallons of orange paint.
Related Links:
Math
What is a Ratio?
What is a proportion?
Unit Rates
Ratios
Fractions
Factors