Multiplication and division are inverse operations. When we divide by 2, we could also solve the same problem by multiplying by ½ .

Think about 36 ÷ 2, which is equal 18. Half of 36, or 36 x ½ is also 18.

We can use this property to help us divide fractions.

Method 1:

Multiply by the reciprocal, also sometimes referred to as "Keep, Change, Flip."

Here is how it works. You rewrite the division question as a multiplication question by flipping the second fraction over.

Example #1:

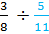
Rewrite this question as

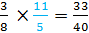
So

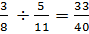
Example #2:

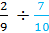
Rewrite this question as

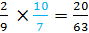
So

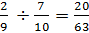
Example #3:

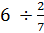
Rewrite the whole number as a fraction first. 6

Then change the question to

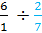
Next, keep the first number, change the division to multiplication and then flip the second fraction over.





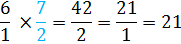
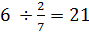
Example #4:

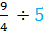
Start by writing 5 as a fraction. 5

Now we can rewrite the question as a multiplication problem.



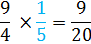
So

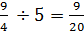
There are other methods for dividing fractions if you cannot remember these steps.

Method 2:

Get common denominators and then divide the numerators.

Example #5:

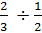
Start by rewriting the problem with common denominators. The best denominator is 6.





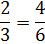
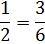
Now that we have common denominators we can just divide the numerators.



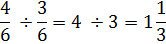
Let's go through the steps one more time.

Example #6:

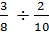
The lowest common denominator for this example would be 40.





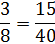
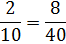
Now we are ready to divide.



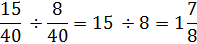
This method does work, but it requires common denominators before you can solve. This first option does not require common denominators, but you do have to remember to flip the second fraction and change the problem to multiplication.


Related Links:
Math
Fractions
Fraction Division Worksheets
Math Vocabulary - Division and Fractions Quiz
Convert Decimals to Fractions Quiz
Compare & Order Fractions Quiz
Multiply Fractions Quiz
Dividing Fractions Quiz
Factors