Parametric Equations: Eliminating Angle Parameters

In a parametric equation the parameter can represent anything including an angle. Just as with non-angle parameters, when the parameter is an angle θ the plane curve can be graphed by selecting values for the angle and calculating the x- and y-values.

x = 5 sin θ, y = 3 cos θ, when $- π \leq θ \leq - \frac{π}{6}$

Angle, θ

$- π$

$- \frac{π}{2}$

$- \frac{π}{3}$

$- \frac{π}{4}$

$- \frac{π}{6}$

$\frac{x}{5} = \sin θ$

-5

$\frac{- 5 \sqrt{3}}{2}$

$\frac{- 5 \sqrt{2}}{2}$

$- \frac{5}{2}$

$\frac{y}{3} = \cos θ$

-3

$\frac{3}{2}$

$\frac{- 3 \sqrt{2}}{2}$

$\frac{- 3 \sqrt{3}}{2}$

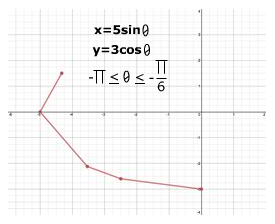
Likewise the overall behavior of the graph can be determined by eliminating the angle parameter.

To eliminate the angle parameter, rewrite the parametric equations in terms that can be substituted into a trigonometric identity.

TRIGONOMETRIC IDENTITIES:

$\sin^{2} θ + \cos^{2} θ = 1$

$\sec^{2} θ - \tan^{2} θ = 1$

$\csc^{2} θ - \cot^{2} θ = 1$

To eliminate the angle parameter of the two parametric equations above, rewrite the equations in terms of sin θ and cos θ and use trigonometric identity

\sin^{2} θ + \cos^{2} θ = 1

$x = 5 \sin θ \to \frac{x}{5} = \sin θ$

$y = 3 \cos θ \to \frac{y}{3} = \cos θ$

Substitute the results into the identity

\sin^{2} θ + \cos^{2} θ = 1

$\sin^{2} θ + \cos^{2} θ = 1 \to {(\frac{x}{5})}^{2} + {(\frac{y}{3})}^{2} = 1$

Then simplify the equation.

$\frac{x^{2}}{5^{2}} + \frac{y^{2}}{3^{2}} = 1$

This resulting rectangular equation represents an ellipse with center (0, 0), vertices (-5, 0) and (5, 0) and minor axis of length 2b = 2 · 3 = 6.

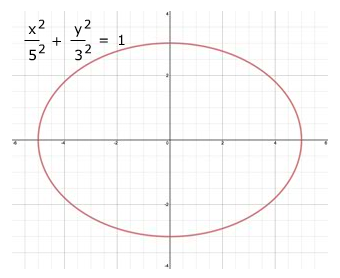
The graph of the rectangular equations shows the overall behavior but the parametric equations are still necessary to describe the parameter and the orientation of the curve.

GUIDELINES FOR ELIMINATING THE ANGLE PARAMETER:

1. Rewrite the parametric equations in terms that can be substituted into one of the trigonometric identities.

2. Substitute the resulting expression into the corresponding trigonometric identity.

$\sin^{2} θ + \cos^{2} θ = 1$

$\sec^{2} θ - \tan^{2} θ = 1$

$\csc^{2} θ - \cot^{2} θ = 1$

3. Simplify

Let's try a couple of examples.

Example 1: Find the rectangular form of the following parametric equations by eliminating the angle and describe the graph.

x = 6 + 2 \cos θ

y = 5 + 2 \sin θ

Step 1: Rewrite the parametric equations in terms that can be substituted into a trigonometric identity.

In this case solve in terms of cos θ and sin θ and use the identity sin² θ + cos² θ = 1.

1^st parametric equation

x = 6 + 2cos θ Original

x - 6 = 2cos θ Subtract 6

$\frac{x - 6}{2} = \cos θ$ Divide by 2

2^nd parametric equation

$y = 5 + 2 \sin θ$ Original

$y - 5 = 2 \sin θ$ Subtract 5

$\frac{y - 5}{2} = \sin θ$ Divide by 2

Step 2: Substitute the resulting expression into the appropriate trigonometric identity.

$\sin^{2} θ + \cos^{2} θ = 1$

$\sin^{2} θ + \cos^{2} θ = 1$ Trig. identity

${(\frac{y - 5}{2})}^{2} + {(\frac{x - 6}{2})}^{2} = 1$ Substitute

$\frac{{(y - 5)}^{2}}{4} + \frac{{(x - 6)}^{2}}{4} = 1$ Square

${(y - 5)}^{2} + {(x - 6)}^{2} = 4$ Multiply by 4

Step 3: Describe the graph

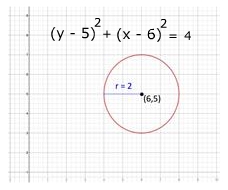
The graph is a circle with center at (6, 5) and radius 2.

Example 2: Find the rectangular form of the following parametric equations by eliminating the angle and describe the graph.

x = 1 + 4 \sec θ

y = 5 \tan θ

Step 1: Rewrite the parametric equations in terms that can be substituted into a trigonometric identity.

In this case solve in terms of sec θ and tan θand use the identity $\sec^{2} θ - \tan^{2} θ = 1$ .

1^st parametric equation

$x = 1 + 4 \sec θ$ Original

$x - 1 = 4 \sec θ$ Subtract 1

$\frac{x - 1}{4} = \sec θ$ Divide by 4

2^nd parametric equation

$y = 5 \tan θ$ Original

$\frac{y}{5} = \tan θ$ Divide by 5

Step 2: Substitute the resulting expression into the appropriate trigonometric identity.

$\sec^{2} θ - \tan^{2} θ = 1$

$\sec^{2} θ - \tan^{2} θ = 1$ Trig. identity

${(\frac{x - 1}{4})}^{2} + {(\frac{y}{5})}^{2} = 1$ Substitute

$\frac{{(x - 1)}^{2}}{4^{2}} + \frac{y^{2}}{5^{2}} = 1$ Square

Step 3: Describe the graph

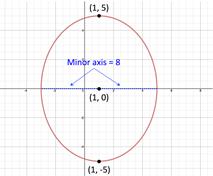
The graph is a hyperbola with center at (1, 0), vertices (1, 5) and (1, -5) and minor axis 2b = 2 · 4 = 8.

To link to this Parametric Equations: Eliminating Angle Parameters page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/parametric_equations_eliminating_angle_parameters/">Parametric Equations: Eliminating Angle Parameters</a>

Parametric Equations: Eliminating Angle Parameters

More Topics

Educational Videos