Ellipse: Standard Equation
DEFINITION OF AN ELLIPSE:
The set of all points (x, y) in a plane the sum of whose distances from two fixed points, called foci, is constant.
Figure 1 shows a picture of an ellipse:
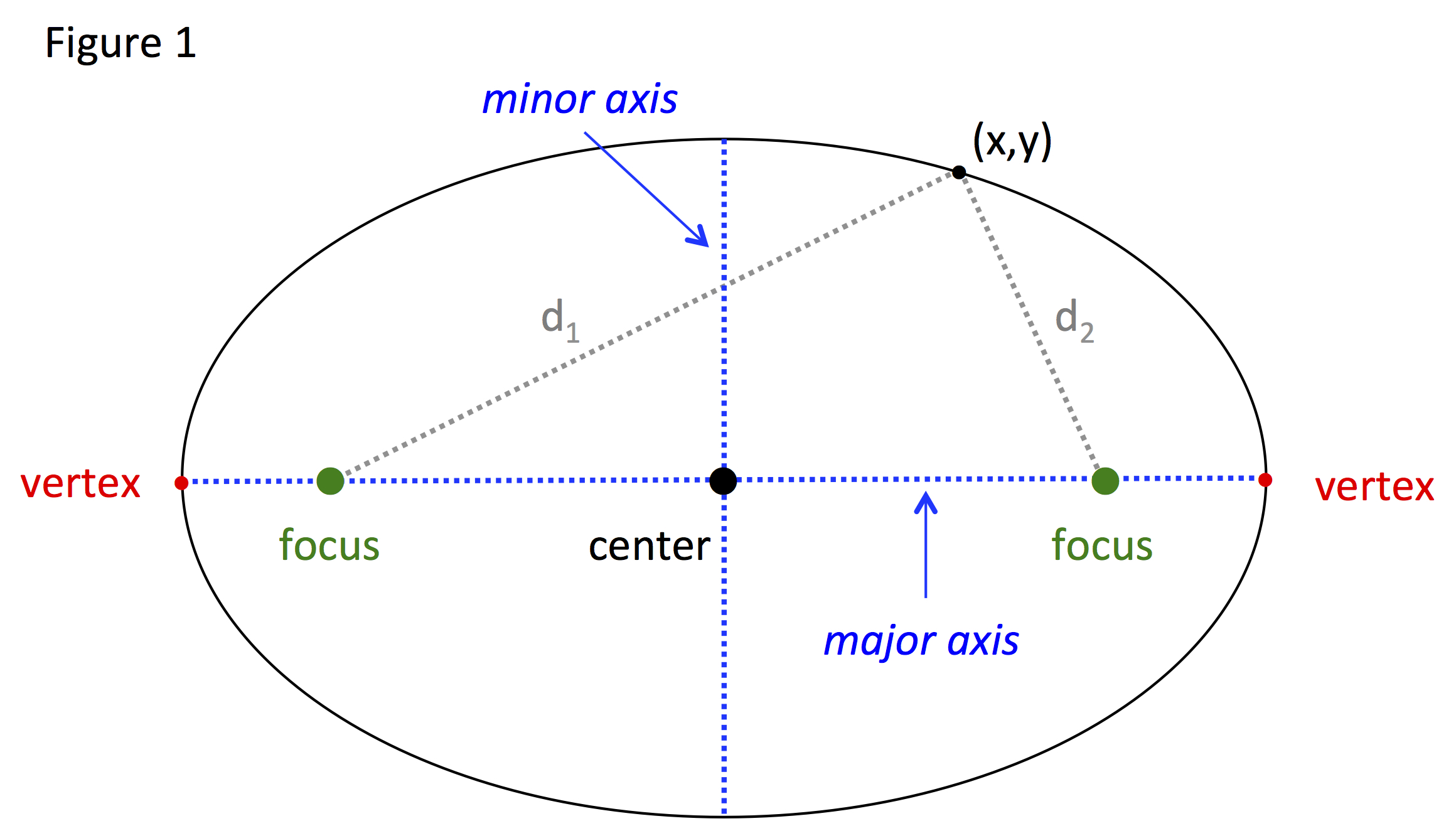
Thus for all (x, y), d1 + d2 = constant. When talking about an ellipse, the following terms are used:
- The foci are two fixed points equidistant from the center of the ellipse.
- The vertices are the points on the ellipse that fall on the line containing the foci.
- The line segment or chord joining the vertices is the major axis.
- The midpoint of the major axis is the center.
- The axis perpendicular to the major axis is the minor axis.
Figure 1 shows an ellipse with a horizontal major axis. However an ellipse could also have a major axis that is vertical as shown in Figure 2.
The standard equation of an ellipse is:
STANDARD EQUATION OF AN ELLIPSE:
➢ Center coordinates (h, k)
➢ Major axis 2a
➢ Major axis 2b
➢ 0 < b < a
major axis is horizontal
major axis is vertical
The foci lie on the major axis, c units from the center, with c2 = a2 - b2.
Let's use these equations in some examples:
|
Step 1: Determine the following: ➢ The coordinates of the center (h, k). ➢ The distance of half the minor axis (b). ➢ The length of half the major axis (a). ➢ The orientation of the major axis. |
Center: Since the foci are equidistant from the center of the ellipse the center can be determine by finding the midpoint of the foci.
Length of b: The minor axis is given as 10, which is equal to 2b.
Length of a: To find a the equation c2 = a2 + b2 can be used but the value of c must be determined. Since c is the distance from the foci to the center, take either foci and determine the distance to the center. Then solve for a. Foci (2, 1): Foci (-4, 1): c = 3
Orientation of major axis: Since the two foci fall on the horizontal line y = 1, the major axis is horizontal. |
|
Step 2: Substitute the values for h, k, a and b into the equation for an ellipse with a horizontal major axis. |
Horizontal major axis equation:
Substitute values:
Simplify:
|
|
Step 1: Group the x- and y-terms on the left-hand side of the equation. |
x2 + 3y2 - 4x - 18y + 4 = 0
|
|
Step 2: Move the constant term to the right-hand side. |
|
|
Step 3: Complete the square for the x- and y-groups. |
Complete the square for the x-group (x2 - 4x) Take the coefficient of the x-term, divide by 2 and square the result.
Add the result to the x-group. (x2 - 4x + 4) Complete the square for the y-group (3y2 - 18y) Factor out a 3 so they y2-coefficient is 1 3(y2 - 6y) Take the coefficient of the y-term, divide by 2 and square the result.
Add the result to the y-group. 3(y2 - 6y + 9) Final result.
|
|
Step 4: Add whatever was added to the left-hand side to the right-hand side. |
|
|
Step 5: Write the x-group and y-group as perfect squares. |
|
|
Step 6: Divide both sides by the value on the right-hand side. |
|
|
Related Links: Math algebra Ellipse: Eccentricity Hyperbola: Standard Equation Pre Calculus |
To link to this Ellipse: Standard Equation page, copy the following code to your site:
