Decomposing a Vector into Components

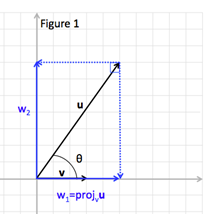
In many applications it is necessary to decompose a vector into the sum of two perpendicular vector components. This is true of many physics applications involving force, work and other vector quantities. Perpendicular vectors have a dot product of zero and are called orthogonal vectors.

Figure 1 shows vectors u and v with vector u decomposed into orthogonal components w₁ and w₂.

Vector u can now be written u = w₁ + w₂, where w₁ is parallel to vector v and w₁ is perpendicular/orthogonal to w₂. The vector component w₁ is also called the projection of vector u onto vector v, proj_v u.

The proj_v u can be calculated as follows:

PROJECTION OF U ONTO V:

Let u and v be nonzero vectors:

$p r o j_{v} u = [\frac{u \cdot v}{v^{2}}] v$

Once the vector component of proj_v uis found, since u = w₁ + w₂, component vector w₂ can be found by subtracting w₁ from u.

w₂ = u - w₁

Let's look at some examples.

To work these examples requires the use of various vector rules. If you are not familiar with a rule go to the associated topic for a review.

Example 1: Let $u = 〈 - 2, 2 〉$ and $v = 〈 3, 5 〉$ . Write vector u as the sum of two orthogonal vectors one of which is a projection of u onto v.

Step 1: Find the proj_v u.

$p r o j_{v} u = [\frac{u \cdot v}{∥ v ∥^{2}}] v = w_{1}$

$p r o j_{v} u = [\frac{u \cdot v}{∥ v ∥^{2}}] v$

$p r o j_{v} u = [\frac{(- 2 \cdot 3) + (2 \cdot 5)}{{\sqrt{3^{2} + 5^{2}}}^{2}}] 〈 3, 5 〉$

$p r o j_{v} u = [\frac{- 6 + 10}{{\sqrt{34}}^{2}}] 〈 3, 5 〉$

$p r o j_{v} u = [\frac{4}{34}] 〈 3, 5 〉 = [\frac{2}{17}] 〈 3, 5 〉$

$p r o j_{v} u = 〈 \frac{6}{17}, \frac{10}{17} 〉$

Step 2: Find the orthogonal component.

w₂ = u - w₁

$w_{2} = 〈 - 2, 2 〉 - 〈 \frac{6}{17}, \frac{10}{17} 〉$

$w_{2} = 〈 (- 2 - \frac{6}{17}), (2 - \frac{10}{17}) 〉$

$w_{2} = 〈 - \frac{40}{17}, \frac{24}{17} 〉$

Step 3: Write the vector as the sum of two orthogonal vectors.

u = w₁ + w₂

$u = 〈 \frac{6}{17}, \frac{10}{17} 〉 + 〈 - \frac{40}{17}, \frac{24}{17} 〉$

Example 2: Given vector $u = 〈 1, 3 〉$ and $v = 〈 - 4, 5 〉$ , write u as a sum of two orthogonal vectors, one which is a projection of u onto v.

Step 1: Find the proj_v u.

$p r o j_{v} u = [\frac{u \cdot v}{∥ v ∥^{2}}] v = w_{1}$

$p r o j_{v} u = [\frac{u \cdot v}{∥ v ∥^{2}}] v$

$p r o j_{v} u = [\frac{(1 \cdot - 4) + (3 \cdot 5)}{{\sqrt{{(- 4)}^{2} + 5^{2}}}^{2}}] 〈 - 4, 5 〉$

$p r o j_{v} u = [\frac{- 4 + 15}{{\sqrt{41}}^{2}}] 〈 - 4, 5 〉$

$p r o j_{v} u = [\frac{11}{41}] 〈 - 4, 5 〉$

$p r o j_{v} u = 〈 - \frac{44}{41}, \frac{55}{41} 〉$

Step 2: Find the orthogonal component.

w₂ = u - w₁

$w_{2} = 〈 1, 3 〉 - 〈 - \frac{44}{41}, \frac{55}{41} 〉$

$w_{2} = 〈 (1 + \frac{44}{41}), (3 - \frac{55}{41}) 〉$

$w_{2} = 〈 \frac{85}{41}, \frac{68}{41} 〉$

Step 3: Write the vector as the sum of two orthogonal vectors.

u = w₁ + w₂

$u = 〈 - \frac{44}{41}, \frac{55}{41} 〉 + 〈 \frac{85}{41}, \frac{68}{41} 〉$

Related Links:
Math
algebra
The First Derivative Rule
The Second Derivative Rule
Pre Calculus

To link to this Decomposing a Vector into Components page, copy the following code to your site:

<a href="https://www.softschools.com/math/pre_calculus/decomposing_a_vector_into_components/">Decomposing a Vector into Components</a>

Decomposing a Vector into Components

More Topics

Educational Videos