Circle: Center-Radius Equation
DEFINITION OF A CIRCLE:
All the points (x, y) in a plane that are equidistant from a fixed center point.
Figure 1 is a circle with the center, radius, and diameter identified.
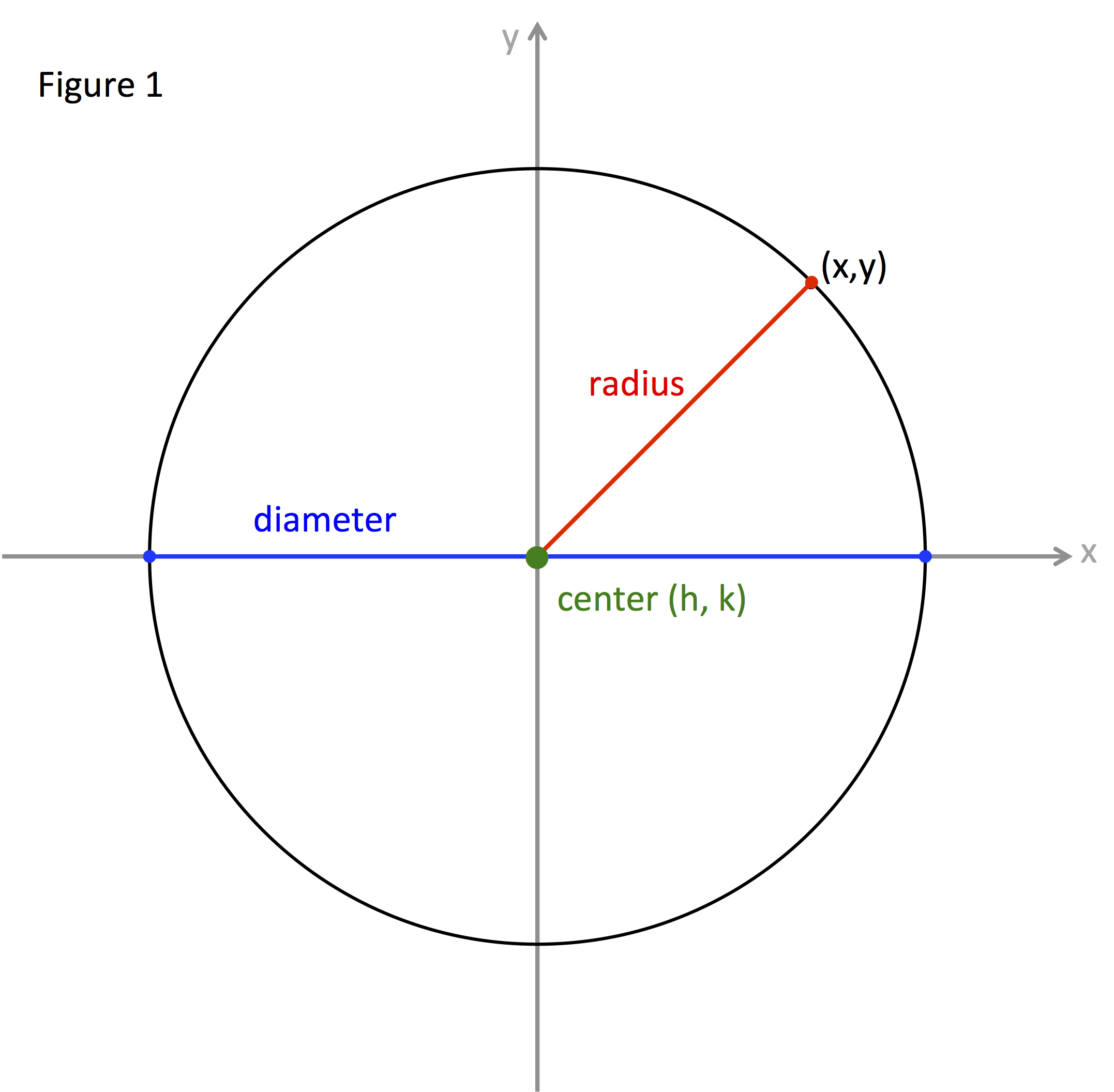
The center is a fixed point in the middle of the circle; usually given the general coordinates (h, k).
The fixed distance from the center to any point on the circle is called the radius.
A line segment from one point on the circle to another point on the circle that passes through the center is twice the radius in length. This line segment is called the diameter of the circle.
A circle can be represented by two different forms of equations, the general form and the center-radius form. This discussion will focus on the center-radius form.
CENTER-RADIUS EQUATION:
Let the center be (h, k) and the radius be r.
Let's use the center-radius equation in some examples:
|
Step 1: Identify the center coordinates and the radius. The center coordinates are given in the problem. The radius must be determined from the diameter, which is 2 times the radius or . |
Center: (-2, 5) Given
|
|
Step 2: Substitute the center coordinates and radius into the center-radius form. Be careful to include negative signs when substituting the center coordinates. |
Original Sub. Simplify |
|
Step 1: Write the center-radius equation for the circle. |
Center: (0, 0) Given Radius = 8 Given Original Sub. Simplify |
|
Step 2: Determine the x-coordinate associated with a y-coordinate of -3. Substitute -3 in for y and solve for x. |
Original Sub. Square Subtract Square Root |
|
Related Links: Math algebra Circle: General Equation Parabola: Standard Equation Pre Calculus |
To link to this Circle: Center-Radius Equation page, copy the following code to your site:
