Writing the Equation of Hyperbolas
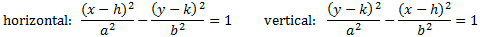
We can write the equation of a hyperbola by following these steps:
1. Identify the center point (h, k)
2. Identify a and c
3. Use the formula c2 = a2 + b2 to find b (or b2)
4. Plug h, k, a, and b into the correct pattern.
5. Simplify
Sometimes you will be given a graph and other times you might just be told some information.
Let's try a few.
1. Find the equation of a hyperbola whose vertices are at (-1, -1) and (-1, 7) and whose foci are at (-1, 8) and (-1, -2).
2. Find the equation of this hyperbola:
To start, let's graph the information we have:
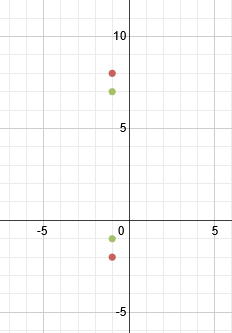
We can tell that it is a vertical hyperbola. Let's find our center point next and mark it. If we want, we can also draw in a rough hyperbola just to make it easier to visualize:
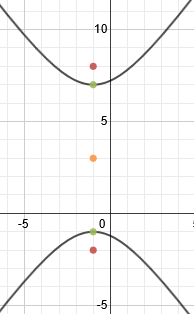
The center point is (-1, 3). To find a, we'll count from the center to either vertex. a = 4. To find c, we'll count from the center to either focus. c = 5
We'll use the formula c2 = a2 + b2 to find b. To do that, we'll sub in a = 4 and c = 5 then solve for b.
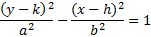
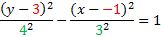
And simplify:
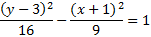

We can tell that it is a vertical hyperbola. Let's find our center point next and mark it. If we want, we can also draw in a rough hyperbola just to make it easier to visualize:

The center point is (-1, 3). To find a, we'll count from the center to either vertex. a = 4. To find c, we'll count from the center to either focus. c = 5
We'll use the formula c2 = a2 + b2 to find b. To do that, we'll sub in a = 4 and c = 5 then solve for b.
c2 = a2 + b2
52 = 42 + b2
25 = 16 + b2
9 = b2 We need to take the square root.
b = 3
We have all our information: h = -1, k = 3, a = 4, b = 3. Since it's a vertical hyperbola, we'll choose that formula and substitute in our information.52 = 42 + b2
25 = 16 + b2
9 = b2 We need to take the square root.
b = 3
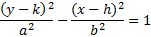
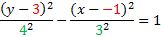
And simplify:
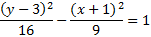
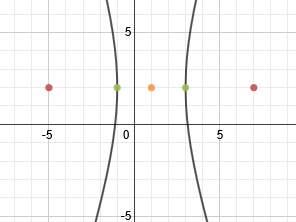
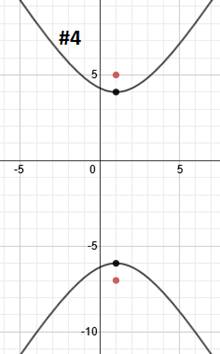
We can tell that it is a horizontal hyperbola. Let's find our center point next and mark it.k

The center point is (1, 2). To find a, we'll count from the center to either vertex. a = 2. To find c, we'll count from the center to either focus. c = 6
We'll use the formula c2 = a2 + b2 to find b. To do that, we'll sub in a = 2 and c = 6 then solve for b.
c2 = a2 + b2
62 = 22 + b2
36 = 4 + b2
32 = b2
To find b, we would need to take the square root, but it won't come out evenly. That's okay, though, because the pattern needs b2, so we can just substitute in 32 for b2.62 = 22 + b2
36 = 4 + b2
32 = b2
We have all our information: h = 1, k = 2, a = 2, b2= 32 . Since it's a horizontal hyperbola, we'll choose that formula and substitute in our information.
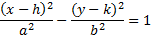
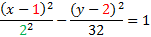
And simplify:
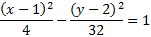
1) Vertices: (2, 1) and (2, -5) Foci: (2, 3) and (2, -7)
2) Vertices: (0, 1) and (6, 1) Foci: (-1, 1) and (7, 1)
3) Vertices: (1, 0) and (3, 0) Foci: (-1, 0) and (5, 0)
2) Vertices: (0, 1) and (6, 1) Foci: (-1, 1) and (7, 1)
3) Vertices: (1, 0) and (3, 0) Foci: (-1, 0) and (5, 0)
Answers:
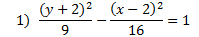
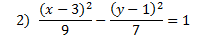
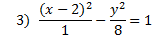
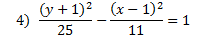
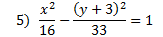
|
Related Links: Math Fractions Factors |
