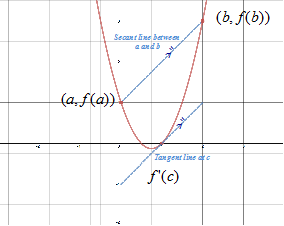
The Mean Value Theorem

Step 1: Determine if the Mean Value Theorem can be applied.

To apply the Mean Value Theorem the function must be continuous on the closed interval and differentiable on the open interval. This function is a polynomial function, which is both continuous and differentiable on the entire real number line and thus meets these conditions.

Step 2: Find the slope of the secant line.

Determine f(a) if a = -1, the left endpoint of the interval.

$f\left(-1\right)={\left(-1\right)}^3+4=3$

$\left(a,f\left(a\right)\right)=\left(-1, 3\right)$

Determine f(b) if b = 1, the right endpoint of the interval.

$f\left(1\right)={\left(1\right)}^3+4=5$

$\left(b,f\left(b\right)\right)=\left(1, 5\right)$

Determine the slope of the secant line between -1 and 1.

$m=\frac{\Delta y}{\Delta x}=\frac{f\left(b\right)-f\left(a\right)}{b-a}=\frac{5-3}{1-\left(-1\right)}=\frac{2}{2}=1$

Step 3: Determine the first derivative of the function.

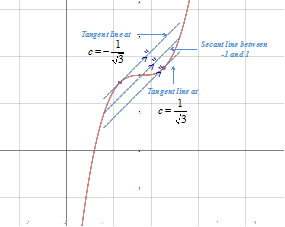
f(x) = x³ + 4

$f^{\prime }\left(x\right)=3x^2$

Step 4: Set $f^{\prime }\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a}$ and solve for c.

$f^{\prime }\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a}$ Mean Value Theorem

$f^{\prime }\left(c\right)=1$     Sub. from Step 2

3c² = 1      Sub. for $f\prime \left(c\right)$

$c^2=\frac{1}{3}$     Divide by 3

$c=\pm \frac{1}{\sqrt{3}}$ Square root

$f\prime \left(\frac{1}{\sqrt{3}}\right)=1$ and $f\prime \left(-\frac{1}{\sqrt{3}}\right)=1$

There are two values of c in the interval of [-1, 1] for which the tangent line of c is parallel to the secant line between -1 and 1.

Step 1: Determine if the Mean Value Theorem can be applied.

To apply the Mean Value Theorem the function must be continuous on the closed interval and differentiable on the open interval. This function is a rational function, which is both continuous on the interval [1, 3]and differentiable on the interval (1, 3).

Step 2: Find the slope of the secant line.

Determine f(a) if a = 1, the left endpoint of the interval.

$f\left(1\right)=\frac{1+3}{1}=4$

$\left(a,f\left(a\right)\right)=\left(1, 4\right)$

Determine f(b) if b = 3, the right endpoint of the interval.

$f\left(3\right)=\frac{3+3}{3}=2$

$\left(b,f\left(b\right)\right)=\left(3, 2\right)$

Determine the slope of the secant line.

$m=\frac{\Delta y}{\Delta x}=\frac{f\left(b\right)-f\left(a\right)}{b-a}=\frac{2-4}{3-1}=\frac{-2}{2}=-1$

Step 3: Determine the first derivative of the function.

$f\left(x\right)=\left(x+3\right)\left(x^{-1}\right)=1+3x^{-1}$

$f^{\prime }\left(x\right)=-3x^{-2}$

Step 4: Set $f^{\prime }\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a}$ and solve for c.

$f^{\prime }\left(c\right)=\frac{f\left(b\right)-f\left(a\right)}{b-a}$   Mean Value Theorem

$f^{\prime }\left(c\right)=-1$    Sub. from Step 2

$-3c^{-2}=-1$   Sub. for $f\prime \left(c\right)$

$c^{-2}=\frac{1}{3}$     Divide by -3

c² = 3 Take reciprocal

$c=\pm \sqrt{3}$    Square root

$f\prime \left(\sqrt{3}\right)=-1$ and $f\prime \left(-\sqrt{3}\right)=1$ (but this point is not in the interval)

There is only one value for c in the interval of [1, 3] for which the tangent line of c is parallel to the secant line between 1 and 3.