Limits: Introduction and One-Sided Limits

The limit of a function f(x) as x approaches some arbitrary value a is denoted by:

$\lim_{x \to a} f (x) = L$

and is read "the limit of f(x) as x approaches a equals L". So as the value of x approaches the value of a, the value of f(x) approaches L. It is important to note that the limit does not include where x = a but only the values close to and on either side of a.

Take the function

f (x) = \frac{x + 2}{x - 1}

as it approaches 1. The table lists the values of f(x) near x = 0.

x	$f (x) = \frac{x + 2}{x - 1}$	x	$f (x) = \frac{x + 2}{x - 1}$
-0.1	-1.72	0.0001	-2.0003
-0.5	-1.8571	0.001	-2.003003
-0.01	-0.1.9702	0.01	-2.030303
-0.001	-1.997003	0.05	-2.157895
-0.0001	-1.9997	0.1	-2.333333

The table shows that as x approaches 0 from either the left or the right, the value of f(x) approaches -2. From this we can guesstimate that the limit of

f (x) = \frac{x + 2}{x - 1}

as x approaches 0 is -2:

$\lim_{x \to 0} \frac{(x + 2)}{x - 1} = - 2$

While the limit of the function

f (x) = \frac{x + 2}{x - 1}

seems to approach -2 as x approaches 0 from either the left or the right, some function have only one-sided limits. The following notation is used to denoted left-hand and right-hand limits.

\lim_{x \to a^{-}} f (x)

\lim_{x \to a^{+}} f (x)

Left-hand limitRight-hand limit

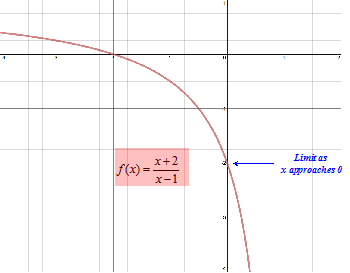
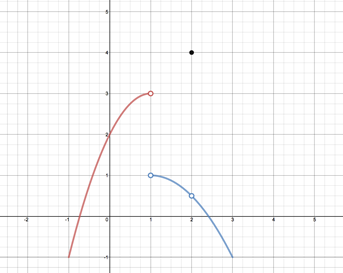
Let's take a look at some limits of the function graphed below.

The limit as x approaches 1 from the left,

\lim_{x \to 1^{-}} f (x)

, is 3 while the limit as x approaches 1 from the right,

\lim_{x \to 1^{+}} f (x)

, is 1. Since the left-hand and right-hand limit as x approaches 1 are different, the limit as x approaches 1 does not exist.

Now' let's look at the limits as x approaches 2. The limit as x approaches 2 from the left is 0.5, and the limit as x approaches 2 from the right is 0.5. Therefore the limit as x approaches 1 from either direction is 0.5.

Note that the when x = 2 the value of the function is 4. Thus the limit is not concerned about the value when x = 2 but only the value as x appraoches 2.

Limits as

x \to 1

Left-hand Limit:    $\lim_{x \to 1^{-}} f (x) = 3$

Right-hand Limit: $\lim_{x \to 1^{+}} f (x) = 1$

Overall Limit:      $\lim_{x \to 1} f (x)$ = DNE

Limits as $x \to 2$

Left-hand Limit:   $\lim_{x \to 2^{-}} f (x) = 0.5$

Right-hand Limit: $\lim_{x \to 2^{+}} f (x) = 0.5$

Overall Limit:     $\lim_{x \to 2} f (x)$ = 0.5

Let's find the limits in a couple examples.

Example 1: Sketch a graph and create a table to determine the limit of the function as $x \to 2$ .

$\lim_{x \to 2} \frac{\sqrt{x - 1} + 3}{x}$

Step 1: Graph the function.

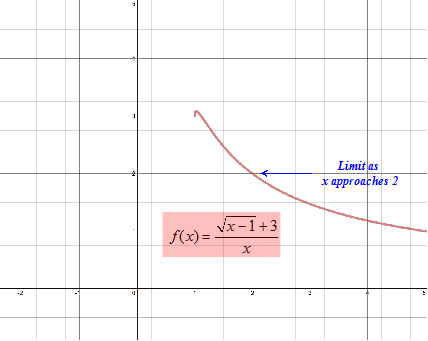
Step 2: Create a table of values close to and on either side of 2.

x	$f (x) = \frac{\sqrt{x - 1} + 3}{x}$	x	$f (x) = \frac{\sqrt{x - 1} + 3}{x}$
1.8	2.1635	2.01	1.9925311
1.9	2.0782	2.05	1.9632659
1.95	2.0382	2.1	1.9280042
1.99	2.0075314	2.2	1.861566

The value as x approaches 2 from both the left and the right approaches 2.

$\lim_{x \to 2^{-}} f (x) = 2$ ; $\lim_{x \to 2^{+}} f (x) = 2$

Step 3: Guesstimate the limit

Since the limit from both the left and the right are the same, then the overall limit as x approaches 2 is 2.

$\lim_{x \to 2} f (x) = 2$ .

Example 2: Sketch a graph and create a table to determine the limit of the function as $x \to 1$ .

$\lim_{x \to 1} \frac{x^{6} + 2}{x^{8} + 1}$

Step 1: Graph the function.

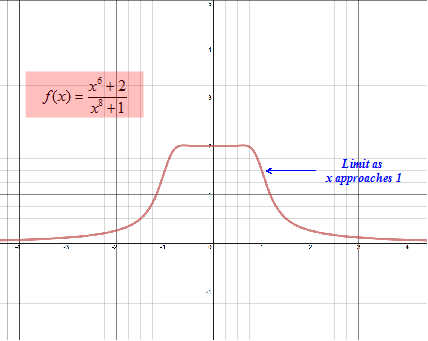
Step 2: Create a table for values close to and on either side of 1.

x	$f (x) = \frac{\sqrt{x - 1} + 3}{x}$	x	$f (x) = \frac{\sqrt{x - 1} + 3}{x}$
0.9	1.7696	1.0001	1.4997
0.99	1.5298	1.001	1.4969
0.999	1.5029	1.01	1.4969
0.9999	1.5003	1.1	1.1997628

The value as x approaches 1 from both the left and the right approaches 1.5.

$\lim_{x \to 1^{-}} f (x) = 1.5$ ; $\lim_{x \to 1^{+}} f (x) = 1.5$

Step 3: Guesstimate the limit

Since the limit from both the left and the right are the same, then the overall limit as x approaches 1 is 1.5.

$\lim_{x \to 1} f (x) = 1.5$ .

Example 3: For the function whose graph is given state the value of each quantity if it exists. If it does not exist, explain why.

$\lim_{x \to 3^{-}} f (x)$ $\lim_{x \to 3^{+}} f (x)$ $\lim_{x \to 3} f (x)$ $f (3)$ $\lim_{x \to 1^{-}} f (x)$ $\lim_{x \to 1^{+}} f (x)$ $\lim_{x \to 1} f (x)$

Graph of Function

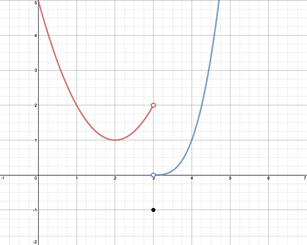
Step 1: Evaluate the limits as x approaches 3.

$\lim_{x \to 3^{-}} f (x)$ - As x approaches 3 from the left, the value of f(x) approaches 2.

$\lim_{x \to 3^{+}} f (x)$ - As 3 approaches 3 from the right, the value of f(x) approaches 0.

$\lim_{x \to 3} f (x)$ - Since the value of f(x) as x approaches 3 from the left does not equal the value as x approaches 3 from the right, this limit does not exist.

Step 2: Evaluate f(3).

The value of y when x is 3 is -1.

f(3) = -1

Notice that the limits of f(x) as $x \to 1$ from the left or right may not be related to the value when x = 1.

Step 3: Evaluate the limits as x approaches 1.

$\lim_{x \to 1^{-}} f (x)$ - As x approaches 1 from the left, the value of f(x) approaches 2.

$\lim_{x \to 1^{+}} f (x)$ - As x approaches 1 from the right, the value of f(x) approaches 2.

$\lim_{x \to 3} f (x)$ - Since the value of f(x) as x approaches 1 from the left equals the value as x approaches 1 from the right, this limit is also 2.

Related Links:
Math
algebra
Limits: Infinite Limits
Limits: Limit Laws
Calculus Topics

To link to this Limits: Introduction and One-Sided Limits page, copy the following code to your site:

<a href="https://www.softschools.com/math/calculus/introduction_and_one_sided_limits/">Limits: Introduction and One-Sided Limits </a>

Limits: Introduction and One-Sided Limits

More Topics

Educational Videos