Limits: Infinite Limits

To discuss infinite limits, let's investiagte the funtion

f (x) = \frac{5}{x - 1}

. Looking at the graph of this function shown here, you can see that as

x \to 1^{-}

the value of f(x) decreases without bound and when

x \to 1^{+}

the value of f(x) increases without bound. A table of values will show the same behavior.

x	$f (x) = \frac{5}{x - 1}$	x	$f (x) = \frac{5}{x - 1}$
0.9	-50	1.00001	500,000
0.99	-500	1.0001	50,000
0.999	-5000	1.001	5000
0.9999	-50,000	1.01	500
0.99999	-500,000	1.1	50

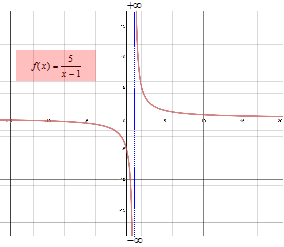
A limit in which f(x) increases or decreases without bound as the value of x approaches an arbitrary number c is called an infinite limit.

This does not mean that a limit exists or that

\infty

is a number. In fact the limit does not exist. The values of

\pm \infty

simply tell how the limit fails to exist because the values as x approaches c increase/decrease without bound.

Infinite limits are denoted by:

$\lim_{x \to a} f (x) = \infty$

and is read "the limit of f(x) as x approaches a is infinity".

DEFINITION OF AN INFINITE LIMIT

Let f(x) be a function that can be defined on either side of a point a, and may or may not be defined at a:

$\lim_{x \to a} f (x) = + \infty$ or $\lim_{x \to a} f (x) = - \infty$

means as x approaches a, but not equal to a, the value of f(x) increase/decreases without bound.

The line at which the limit of a function increases or decreases without bound is called a vertical asymptote.

DEFINITION OF A VERTICAL ASYMPTOTE

The line x = a is a vertical asymptote of f(x) if one of the following is true:

$\lim_{x \to a} f (x) = \infty$ $\lim_{x \to a^{-}} f (x) = \infty$ $\lim_{x \to a^{+}} f (x) = \infty$

$\lim_{x \to a} f (x) = - \infty$ $\lim_{x \to a^{-}} f (x) = - \infty$ $\lim_{x \to a^{+}} f (x) = - \infty$

Let's find the infinite limits in a couple examples.

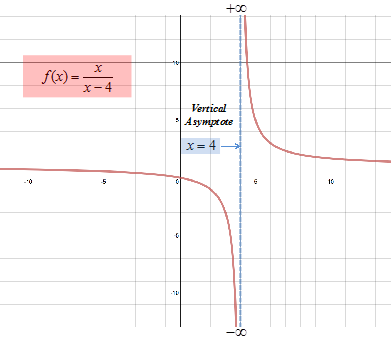
Example 1: Find the $\lim_{x \to 4^{+}} \frac{x}{x - 4}$ and $\lim_{x \to 4^{-}} \frac{x}{x - 4}$ , sketch the graph and define the vertical asymptote.

Step 1: Find the $\lim_{x \to 4^{+}} \frac{x}{x - 4}$

Create a table of values for f(x) as $x \to 4^{+}$ or justify the behavior of the values for f(x). Do not include x = 4.

x	$\frac{x}{x - 4}$
4.1	41
4.01	401
4.001	4001
4.0001	40,001

As values for x get closer and closer to 4 but remain larger than 4, the denominator becomes a smaller and smaller positive number so the quotient becomes increasingly larger without bound.

$\lim_{x \to 4^{+}} \frac{x}{x - 4} = \infty$

Step 2: Find the $\lim_{x \to 4^{-}} \frac{x}{x - 4}$

Create a table of values for f(x) as $x \to 4^{-}$ or justify the behavior of the values for f(x). Do not include x = 4.

x	$\frac{x}{x - 4}$
3.9	-39
3.99	-399
3.999	-3999
3.9999	39,999

As values for x get closer and closer to 4 but remain smaller than 4, the denominator becomes a smaller and smaller negative number so the quotient becomes increasingly large negative number without bound.

$\lim_{x \to 4^{-}} \frac{x}{x - 4} = - \infty$

Step 3: Sketch the graph.

Step 4: Define the vertical asymptote.

Because $\lim_{x \to 4^{-}} f (x) = - \infty$ ; $\lim_{x \to 4^{+}} f (x) = \infty$ , the line $x = 4$ is a vertical asymptote.

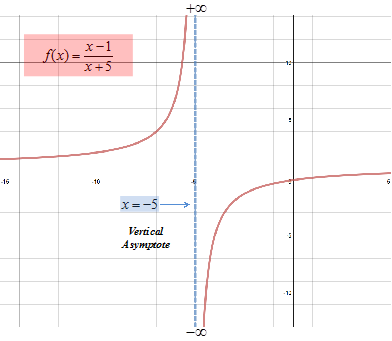
Example 2: Find the $\lim_{x \to - 5} \frac{x - 1}{x + 5}$ if it exists. If it does not exist explain why.

Step 1: Find the $\lim_{x \to - 5^{+}} \frac{x - 1}{x + 5}$

Create a table of values for f(x) as $x \to - 5$ or justify the behavior of the values for f(x). Do not include x = -5.

x	$\frac{x - 1}{x + 5}$
-4.9	-59
-4.99	-599
-4.999	-5999
-4.9999	-59,999

As values for x get closer and closer to -5 but remain larger than -5, the denominator becomes a smaller and smaller positive number while the numerator approaches -6 so the quotient becomes increasingly negative without bound.

$\lim_{x \to 5^{+}} \frac{x - 1}{x + 5} = - \infty$

Step 2: Find the $\lim_{x \to - 5^{-}} \frac{x - 1}{x + 5}$

Create a table of values for f(x) as $x \to - 5^{-}$ or justify the behavior of the values for f(x). Do not include x = -5.

x	$\frac{x - 1}{x + 5}$
-5.1	61
-5.01	601
-5.001	6001
-5.0001	60,001

As values for x get closer and closer to -5 but remain smaller than -5, the denominator becomes a smaller and smaller negative number while the numerator approaches -6 so the quotient becomes an increasingly larger positive number without bound.

$\lim_{x \to - 5^{-}} \frac{x - 1}{x + 5} = \infty$

Step 3: Sketch the graph.

Step 4: Determine if the function has a limit.

Because $\lim_{x \to - 5^{-}} f (x) = \infty$ ; $\lim_{x \to - 5^{+}} f (x) = - \infty$ , the line $x = - 5$ is a vertical asymptote. Because the limits increase without bound, no limit exists. Remember, an infinite limit is not a limit but merely states how the limit fails.

Related Links:
Math
algebra
Limits: Limit Laws
General Differentiation Rules
Calculus Topics

To link to this Limits: Infinite Limits page, copy the following code to your site:

<a href="https://www.softschools.com/math/calculus/infinite_limits/">Limits: Infinite Limits </a>

Limits: Infinite Limits

More Topics

Educational Videos