Finding Vertical Asymptotes of Rational Functions
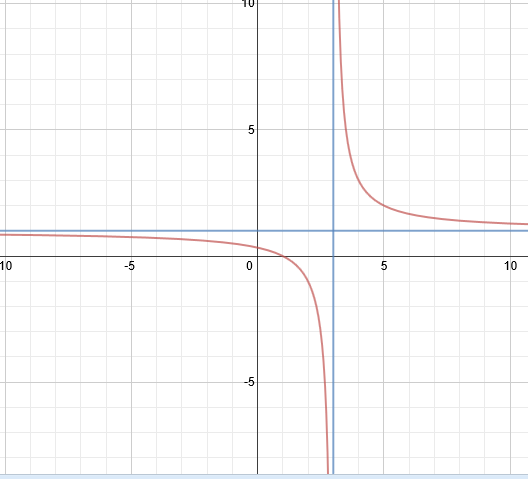
In this example, there is a vertical asymptote at x = 3 and a horizontal asymptote at y = 1. The curves approach these asymptotes but never cross them.
To find the vertical asymptote(s) of a rational function, simply set the denominator equal to 0 and solve for x.
Examples: Find the vertical asymptote(s)
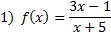
We mus set the denominator equal to 0 and solve:
x + 5 = 0
x = -5
There is a vertical asymptote at x = -5
x + 5 = 0
x = -5
There is a vertical asymptote at x = -5
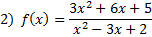
We mus set the denominator equal to 0 and solve:
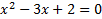
This quadratic can most easily be solved by factoring the trinomial and setting the factors equal to 0.
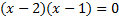


There are vertical asymptotes at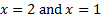 .
.
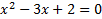
This quadratic can most easily be solved by factoring the trinomial and setting the factors equal to 0.
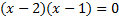


There are vertical asymptotes at
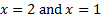 .
.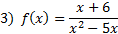
We mus set the denominator equal to 0 and solve:
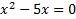
This quadratic can most easily be solved by factoring out the x and setting the factors equal to 0.
x(x - 5) = 0
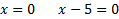

There are vertical asymptotes at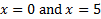 .
.
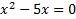
This quadratic can most easily be solved by factoring out the x and setting the factors equal to 0.
x(x - 5) = 0
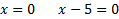

There are vertical asymptotes at
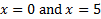 .
.Practice: Find the vertical asymptote(s) for each rational function:
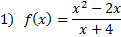
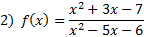
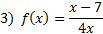
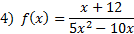
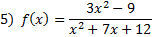
Answers: 1) x = -4 2) x = 6 and x = -1 3) x = 0 4) x = 0 and x = 2 5) x = -3 and x = -4
|
Related Links: Math Fractions Factors |
