Home > Math > Calculus >Distinguishing Conic Sections From Graphing Format

Distinguishing Conic Sections From Graphing Format

Sometimes you will be told which conic section (circle, parabola, ellipse, or hyperbola) you need to graph. Other times, you will simply be given an equation. In these cases, you need to start by determining which conic section you are looking at.

Let's review the patterns for each conic section:

Circle: (x-h)2+(y-k)2=r2
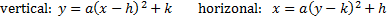
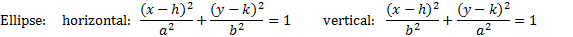
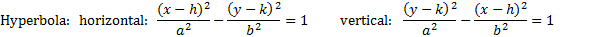
Parabola:  



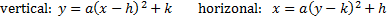
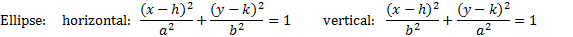
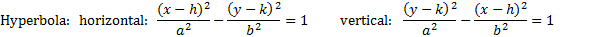
Let's note a few key differences:

To complete the square for ellipses and hyperbolas:

  • Parabolas only have one squared variable. (For all the others, both the x and y are squared.)
  • Circles do not have fractions/denominators. Also, they may or may not equal 1.
  • Ellipses have different denominators and equal 1. There is a plus sign in between the fractions.
  • Hyperbolas also have different denominators and equal 1, but there is a negative sign in between the fractions.

Let's identify a few conic sections:


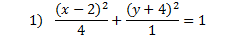
This is an ellipse because both variables are squared, it contains fractions, it equals 1, and there is a plus sign in between the fractions.

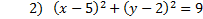
This is a circle. You can tell because both variables are squared but there are not fractions.

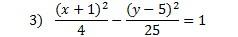
This is a hyperbola because both variables are squared, it contains fractions, it equals 1, and there is a negative sign in between the fractions.

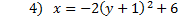
We know this is a parabola because only the y is squared.
Identify each equation as a parabola, circle, ellipse, or hyperbola.






Answers: 1) parabola    2) hyperbola    3) ellipse    4) circle   5) hyperbola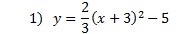

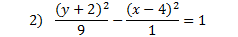
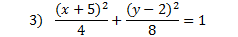
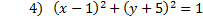
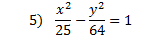
Related Links:
Math
Fractions
Factors