Simplifying Radical Expressions
|
Radical expressions (expressions with square roots) need to be left as simplified as possible. Here's how to simplify a rational expression
1) Factor the radicand (the number inside the square root) into its prime factors 2) Bring any factor listed twice in the radicand to the outside. Examples:
1) 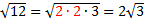 First we factored 12 to get its prime factors. Then, since there were two 2's inside the square root, we brought the 2 to the outside (because the square root of 2.2 is 2). 2) 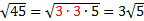 First we factored 45 to get its prime factors. Then, since there were two 3's inside the square root, we brought the 3 to the outside. 3) 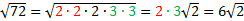 In this example, we could remove both a 2 and a 3. Notice that the last 2 is left inside since we can only remove a number if there are two of them. Practice: Simplify the following rational expressions.
1) 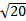 2) 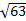 3) 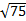 4) 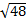 5) 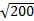 Answers: 1) 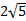 2) 2)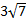 3) 3)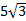 4) 4)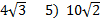 |
|
Related Links: Math Algebra Factors |
