Factoring Trinomials
|
Remember that the first step in factoring is always to look for common factors and factor them out. After you look for common factors, if you have a trinomial that looks something like this: 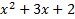 ,then you want to the following process: ,then you want to the following process:
1) Check for common factors & factor them out 2) Set up 2 parenthesis 3) Factor the first term into possible factors 4) Factor the last term into possible factors. Remember to include negative options. 5) Choose the correct set of factors to give you the middle term (you are looking for the set that when you add them gives you the middle number). 6) Write those factors in the parenthesis 7) Check your answer by multiplying out the answer (you can use FOIL) and making sure it matches the original problem Examples:
1) 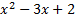 There are no common factors, so we set up our parenthesis. There are no common factors, so we set up our parenthesis.  Next we factor the first term.
Next we factor the first term.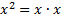 .This is the only choice, so we know this is the right set and we can list these in the front of .This is the only choice, so we know this is the right set and we can list these in the front of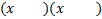 each parenthesis each parenthesisNow we factor the last term: 2. There are two choices: 2(1)and -2(-1).We must choose which set of factors will work. To do this, we need to add them together and see which one equals the middle term's coefficient -3.
For 2(1), 2 + 1 = 3 not -3, so this is not the right set For -2(-1),-2 + (-1) = -3 , so this is the one we're looking for 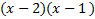 Write our set of factors -2(-1) one in the first parenthesis and Write our set of factors -2(-1) one in the first parenthesis and one in the second. Remember to include the signs.We can check our answer. Final answer: 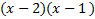
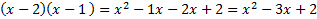 . This
. This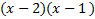 matches the original, so we factored correctly. matches the original, so we factored correctly.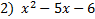 There are no common factors, so we set up our parenthesis.
There are no common factors, so we set up our parenthesis. Next we factor the first term.
Next we factor the first term. 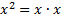 . This is the only choice, so we know this is the right set and we can list these in the front of . This is the only choice, so we know this is the right set and we can list these in the front of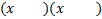 each parenthesis
each parenthesis
Now we factor the last term: -6. There are four choices:
6(-1)-6(1 )-3(2)3(-2). We must choose which set of factors will work. To do this, we need to add them together and see which one equals the middle term's coefficient -5. For 6(-1),6+(-1)=5. This is no good. For -6(1),-6+(1)=-5. This is the one we need, so we don't have to waste time trying the rest. Write our set of factors -6(1) one in the first parenthesis and one in the second. Remember to include the signs. 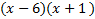 We can check our answer. We can check our answer. 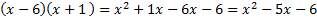 . This matches the original, so we factored correctly.
. This matches the original, so we factored correctly.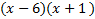
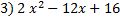 There is a common factor of 2, so we must factor that out first.
There is a common factor of 2, so we must factor that out first.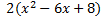 Next we factor the first term. Next we factor the first term. 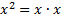 . Notice of that we just . Notice of that we just 2 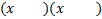 bring the 2 down, but it won't affect the rest of the factoring.
bring the 2 down, but it won't affect the rest of the factoring.
Now we factor the last term: 8. There are four choices:
8(1)-8(-1 )4(2)-4(-2). We must find out which set adds up to the middle coefficient, -6 . (notice we're looking at the factored trinomial, not the original.) Can you find the one that works? 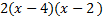
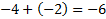 , so this is our set. Put them in the parenthesis.We can check our answer. , so this is our set. Put them in the parenthesis.We can check our answer. Final answer: 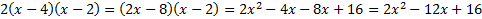 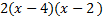 This matches the original, so we factored correctly.
This matches the original, so we factored correctly.Practice:
1)
Answers:
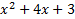 2) 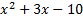 3) 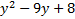 4) 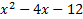 5) 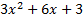 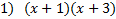
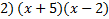
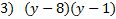
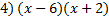
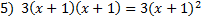 |
