Time Dilation Formula

Special relativity states that time can pass at different rates in different reference frames. The time depends on the velocity of one reference frame relative to another. In one reference frame, two events (for example, two ticks of a clock) will occur at the same position. In this reference frame, the time between the events is called one-position time or proper time, and is labeled Δt₀. In another reference frame, an observer will see the two events happen in different positions. In the observer's reference frame, the time between events is called two-position time or observer time, and is labeled Δt. The observer time is always larger than the proper time. This effect is called time dilation. Both Δt₀ and Δt are measured in seconds (s).

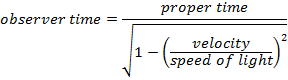
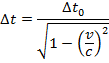
Δt = the observer time, or two-position time (s)

Δt₀ = the proper time, or one-position time (s)

v = velocity (m/s)

c = speed of light (3.0 x 10⁸ m/s)

Time Dilation Formula Questions:

1) Tanya boards a spaceship, and flies past Earth at 0.800 times the speed of light. Her twin sister, Tara, stays on Earth. At the instant Tanya's ship passes Earth, they both start timers. Tanya watches her timer, and after she sees 60.0 seconds have passed, she stops it. At that instant, how much time would Tara's timer say has passed?

Answer: The two events to consider are the starting and stopping of Tanya's timer. In Tanya's reference frame, these two events happen in the same position. That means that Tanya's time aboard the spaceship is the proper (one-position) time, and the time difference aboard the spaceship is Δt₀. The starting and stopping of Tanya's timer happens in two positions in Tara's reference frame, so the time difference on Earth is the observer (two-position) time, Δt. The amount of time that passes in Tara's reference frame can be found using the formula:

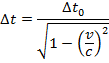
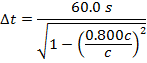
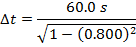
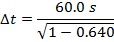
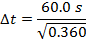
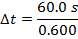
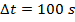
When Tanya is in a reference frame moving at 0.800c relative to Tara's reference frame, and Tanya observes that 60.0 s pass, her sister Tara will observe that 100 s have passed.

2) Cosmic rays colliding with Earth's upper atmosphere produce high-energy particles called muons. An observer detects that a muon has been created, and observes that it reaches the surface of the Earth 20.0 x 10^-6 seconds later. The observer also determines that the muon was moving at 2.97 x 10⁸ m/s. In the muon's reference frame, how much time passed between its creation and reaching the surface of the Earth?

Answer: The two events to consider are the creation of the muon, and it reaching the surface of Earth. In the muon's reference frame, these two events happen in the same position. In the observer's reference frame, these two events happen in different positions. That means the muon's time is the proper (one-position) time, Δt₀. The Earth-based observer's time is Δt. The observer's time is known, and so the amount of time that passes in the muon's reference frame can be found by rearranging the time dilation formula:

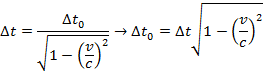
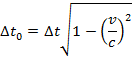
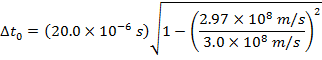
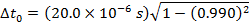
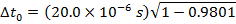
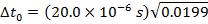
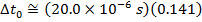
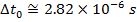
In the muon's reference frame, approximately 2.82 x 10^-6 seconds pass between when the muon is created and when it reaches the Earth's surface.