Snell's Law Formula

When light strikes a smooth barrier between two transparent materials, the light is partly reflected, and partly refracted (transmitted). The formula that describes refraction is also known as Snell's Law. The angle of refraction depends on the angle of incidence of the light, and the indexes of refraction of the two materials. The index of refraction of a material depends on the material's properties. The angles in Snell's Law are always measured relative to the normal to the barrier, which is perpendicular to the barrier's surface. The angles are measured in radians or degrees, and the indexes of refraction are unitless numbers.

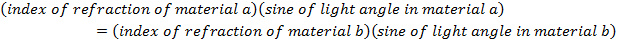
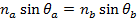
n_a = index of refraction in material a, (unitless)

n_b = index of refraction in material b, (unitless)

θ_a = angle of light relative to normal to the barrier in material a, (radians or degrees)

θ_b = angle of light relative to normal to the barrier in material b, (radians or degrees)

Snell's Law Formula Questions:

1) A beam of light in air makes an angle of 41.8° relative to the normal to the surface of a pool of clear water. The index of refraction for air is 1.000, and the index of refraction for the water is 1.333. What is the angle of the light beam in the water, relative to the normal?

Answer: The angle of the light beam in the water relative to the normal can be found using Snell's Law. As a reminder, the angles in Snell's Law are always measured relative to the normal (perpendicular) to the surface. The angle can be found by rearranging the formula:

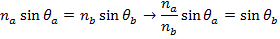
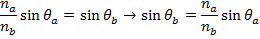
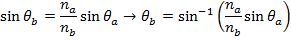
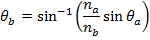
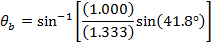
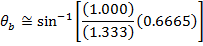
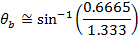
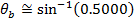
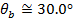
The angle of the light beam in the water (relative to the normal) is 30.0°.

2) A beam of light in air makes an angle of 30.0° relative to the surface of a diamond. The index of refraction for air is 1.000, and the index of refraction for diamond is 2.417. What is the angle of the light beam in the diamond, relative to the surface?

Answer: The angles in Snell's Law are always measured relative to the normal (perpendicular). In this question, the angle of the beam in air is given relative to the surface. The normal is at a 90° angle to the surface, so the angle in air relative to the normal is:

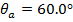
Snell's Law can be used to find θ_b, which is the angle of the beam in the diamond, relative to the normal. The angle θ_b can be found by rearranging the formula:

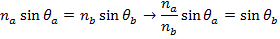
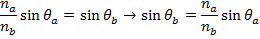
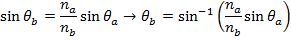
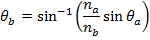
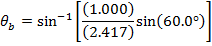
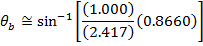
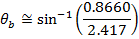
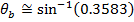
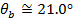
The question asks for the angle of the light beam in the diamond, relative to the surface. The angle θ_b is the angle relative to the normal. If we label the angle relative to the surface a (Greek letter "alpha"), its value is:

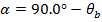
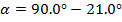
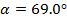
The angle of the light beam in the diamond, relative to the surface, is 69.0°.