Simple Harmonic Motion Formula

Simple Harmonic Motion (SHM) is a special type of periodic motion that follows a certain pattern. The position of an object in simple harmonic motion is described by a sine function that depends on an amplitude of the motion A, an angular frequency 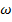, time t, and a starting condition called the phase shift 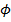. The unit for position and amplitude is meters (m), the unit for angular frequency is radians/s, the unit for time is seconds (s), and the unit for the phase shift is radians.

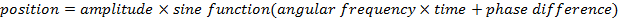
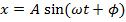
x = position (m)

A = amplitude (m)

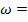angular frequency (radians/s)

t = time (s)

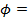phase shift (radians)

Simple Harmonic Motion Formula Questions:

1) A ball on a spring is pulled and released, which sets the ball into simple harmonic motion. The amplitude of the ball's motion is 0.080 m, and the phase shift is 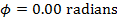. If the angular frequency of the ball's motion is 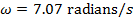, what will be the ball's position at time t = 2.00 s?

Answer: The amplitude of the ball's motion is A = 0.080 m. The position of the ball relative to equilibrium is x, and can be found from the formula:

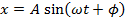
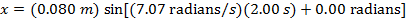
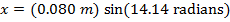
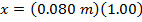
x = 0.080 m

At time t = 2.00 s, the ball will be at position x = 0.080 m relative to the equilibrium position.

2) A bee is flying back and forth over a flower, moving in a pattern that can be described by simple harmonic motion. The equilibrium position is the center of the flower. At time t = 0.00 s, the bee is at position x = -0.020 m. The amplitude of the bee's motion is A = 0.020 m, and the angular velocity is 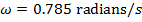. What will be the position of the bee at time t = 4.00 s?

Answer: The first step to solving this problem is to calculate the phase shift 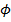. Rather than provide the phase shift value, initial conditions were given. The initial conditions can be used with the simple harmonic motion formula to calculate the phase shift:

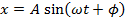
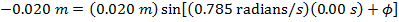
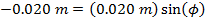
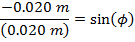
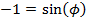
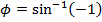
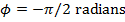
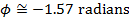
The next step to finding the bee's position at time t = 4.00 s is to substitute the known values, including the value of the phase shift, in to the simple harmonic motion formula:

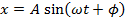
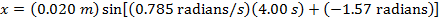
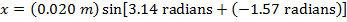
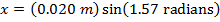
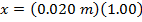
x = 0.020 m

The position of the bee at t = 4.00 s is 0.020 m.