Resistors in Series Formula

In electric circuits, it is often possible to replace a group of resistors with a single, equivalent resistor. The equivalent resistance of a number of resistors in series is the sum of the individual resistance values. The unit of resistance is the Ohm (Ω), which is equal to a Volt per Ampere (1 Ω = 1 V/A). Larger resistors with kilo-Ohm (1 kΩ = 10³ Ω) or mega-Ohm (1 MΩ = 10⁶ Ω) resistances are common, as well.

equivalent resistance = resistor 1 + resistor 2 + resistor 3 + ...

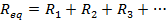
R_eq = equivalent resistance (Ω or larger units)

R₁ = resistance of first resistor (Ω)

R₂ = resistance of second resistor (Ω)

R₃ = resistance of third resistor (Ω)

Resistors in Series Formula Questions:

1) What is the equivalent resistance of a 480.0 kΩ, a 320.0 kΩ, and a 100.0 kΩ resistor connected in series?

Answer: The resistances are all expressed in kilo-Ohms, and so there is no need to change their units. The equivalent resistance can be found in kΩ using the formula:

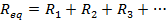
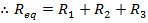
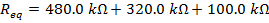
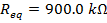
The equivalent resistance of the 480.0 kΩ, 320.0 kΩ, and 100.0 kΩ resistors in series is 900.0 kΩ.

2) Two resistors are connected in series in an electric circuit. Their resistances are 240.0 kΩ, and 8.00 MΩ. What is the equivalent resistance?

Answer: The resistance values are expressed using different units. The first step to finding the equivalent resistance is to convert these to a common unit. One of the values can be converted to the same unit as the other. In this solution, the values will be converted to mega-Ohms.

If R₁ = 240.0 kΩ, and R₂ = 8.00 MΩ, then:

R₁ = 240.0 kΩ

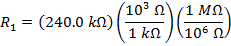
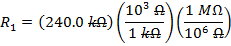
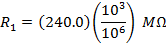
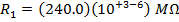
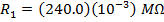
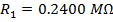
The equivalent resistances can now be found using the formula:

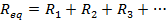
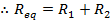
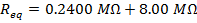
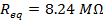
The equivalent resistance of the 240.0 kΩ and 8.00 MΩ resistors in series is 8.24 MΩ.