Potential Energy: Elastic Formula

Potential energy is energy that is stored in a system. There is the possibility, or potential, for it to be converted to kinetic energy. Elastic potential energy is stored in a spring that has been stretched or compressed by a distance x away from its equilibrium position. Position x = 0 must always be the position where the spring is most relaxed. Springs have their own natural "spring constants" that define how stiff they are. The letter k is used for the spring constant, and it has the units N/m. Like all work and energy, the unit of potential energy is the Joule (J), where 1 J = 1 N∙m = 1 kg m²/s² .

potential energy = 1/2(spring constant)(distance from equilibrium)²

U = 1/2kx²

U = potential energy of a spring at a certain position

k = the spring constant, specific to the spring, with units N/m.

x = distance the spring is stretched or compressed away from equilibrium

Potential Energy: Elastic Formula Questions:

1) A spring, which has a spring constant k = 7.50 N/m, has been stretched 0.40 m from its equilibrium position. What is the potential energy now stored in the spring?

Answer: The spring has been stretched x = 0.40 m from equilibrium. The potential energy can be found using the formula:

U = 1/2kx²

U = 1/2(7.50 N/m)(0.40 m)²

U = 0.60 N∙m

U = 0.60 J

The elastic potential energy stored by the spring when it is has been stretched 0.40 m is 0.60 J.

2) A spring with a spring constant k = 800 N/m has been compressed, and 196 J of potential energy is stored. What distance from equilibrium has the spring been compressed?

Answer: The spring constant of the spring is k = 800 N/m, and the potential energy is U = 196 J. To find the distance, rearrange the equation:

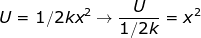
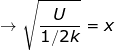
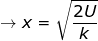
The equation to find the distance the spring has been compressed is therefore:

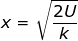
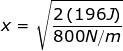
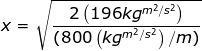
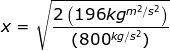
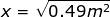
x = 0.70 m

The spring has been compressed 0.70 m, which resulted in an elastic potential energy of U = 196 J being stored.