Period of a Pendulum Formula

Definition: A pendulum is a weight suspended from a pivot that swing with a regular movement. The first scientist that tried to describe the physical phenomenon behind this movement was Galileo Galilei, which in 1602, after he became interested from a chandelier in Pisa Cathedral. He discovered that this movement could be useful to be used as a timekeeper because the time in which a pendulum completes a whole movement from one side to the opposite side is independent on the mass of the pendulum or the width of the swing.

Today, the bases of the movement of pendulum is the base for comprehension of quantum mechanics phenomena such as the harmonic oscillator.

Formula: the period of a pendulum is defined as the time taken to complete a cycle (swing). It depends on the length of the pendulum and the gravity of the place where it is been measured. It also depends on the amplitude that is the maximum angle that a pendulum can swing form the point zero or the vertical axis. The period is called T and the formula is:

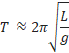
Where L represents the length of the pendulum and g is the value of the acceleration of gravity.

Example: The above formula is the simplest way to calculate the period of a pendulum. And it can be used to get accurate estimation of this value. For calculating the period, you will need to have the length of the pendulum and the local acceleration of gravity.

a) Calculate the period of a pendulum that has a length of 20 cm and is located in Milano.

First, you will need to convert the units to SI, it is meters.

20 cm = 0.2 m

Second, you will need to know the acceleration of gravity in Milano. In general, most place are approximated to 9,8 m/s².

You can use the formula:

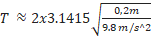= 0.89 s

The unit of period is always in time units: seconds, minutes, hours, etc.