Newton's Law of Cooling Formula

Sir Isaac Newton created a formula to calculate the temperature of an object as it loses heat. The heat moves from the object to its surroundings. The rate of the temperature change is proportional to the temperature difference between the object and its surroundings. The formula can be used to find the temperature at a given time. The SI unit of temperature is the Kelvin (K), but degrees Celsius (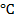) is common.

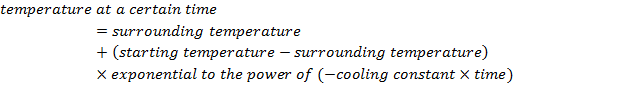
T(t) = T_s + (T₀ - T_s ) e^(-kt)

T(t) = temperature of an object at a certain time (Kelvin, K)

t = time (s)

T_s = temperature of the surroundings (Kelvin, K)

T₀ = starting temperature of the object (Kelvin, K)

k = a cooling constant, specific to the object (1/s)

Newton's Law of Cooling Formula Questions:

1) A pot of soup starts at a temperature of 373.0 K, and the surrounding temperature is 293.0 K. If the cooling constant is k = 0.00150 1/s, what will the temperature of the pot of soup be after 20.0 minutes?

Answer: The soup cools for 20.0 minutes, which is:

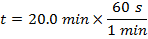
t = 1200 s

T(t) = T_s + (T₀ - T_s ) e^(-kt)

T(1200 s) = 293.0 K + (373.0 K-293.0 K) e^{(-(0.001500 1/s)(1200 s))}

T(1200 s) = 293.0 K + (373.0 K-293.0 K) e^(-1.800)

T(1200 s) = 293.0 K + (373.0 K-293.0 K)(0.1653)

T(1200 s) = 293.0 K + (80.0 K)(0.1653)

T(1200 s) = 293.0 K + 13.224 K

T(1200 s) ≈ 306.224 K

After 20 minutes, the soup's temperature is 306.224 K.

2) A rod of iron is heated in a forge to a temperature of 1280.0K. The rod is then plunged in to a bucket of chilled water with a temperature of 280.0 K. After 10.0 s, the temperature of the iron rod drops to 329.7K. What is the cooling constant for this iron rod in water?

Answer: The cooling constant can be found by rearranging the formula:

T(t) = T_s+(T₀-T_s ) e^(-kt)

∴T(t)- T_s = (T₀-T_s ) e^(-kt)

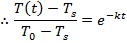
The next step uses the properties of logarithms. The natural logarithm of a value is related to the exponential function (e^x) in the following way: if y = e^x, then lny = x. To continue rearranging the formula, the natural logarithm is applied to both sides:

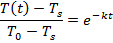
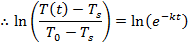
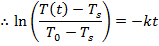
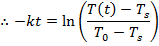
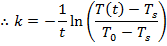
Using this formula for the cooling constant k, the solution can be found:

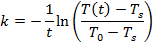
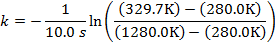
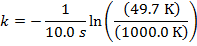
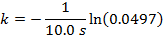
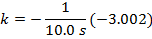
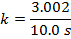
k = 0.300 1/s

The cooling constant for the iron rod in water is k = 0.300 1/s.