Moment of Inertia Formula (common shapes)
The moment of inertia is a value that measures how difficult it is to change the state of an object's rotation. The moment of inertia depends on the mass and shape of an object, and the axis around which it rotates. The moments of inertia for some common shapes can be found using the following formulas. The moment of inertia of an object made of a number of these common shapes is the sum of the moments of inertia of its components. The unit for moment of inertia is the kilogram-meter squared, 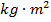 .
.
|
Object Type |
Description |
Formula |
|
Thin rod, axis through the center |
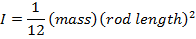
|
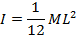
|
|
Thin rod, axis through one end |
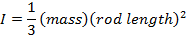
|
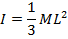
|
|
Rectangular plate, axis through center |
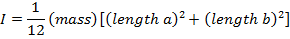
|
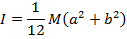
|
|
Rectangular plate, axis along edge |
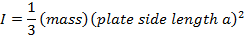
|
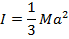
|
|
Hollow cylinder, with a wall thickness |
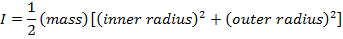
|
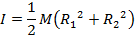
|
|
Solid cylinder |
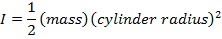
|
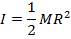
|
|
Thin-walled hollow cylinder |
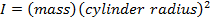
|
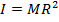
|
|
Solid sphere |
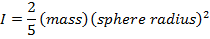
|
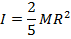
|
|
Thin-walled hollow sphere |
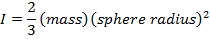
|
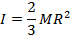
|
I = moment of inertia (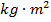 )
)
M = total mass of the rotating object (kg)
L = the total length of the rod (m)
a = the length of two sides of the plate (m)
b = the length of the other two sides of the plate (m)
R1 = the inner radius of the cylinder (m)
R2 = the outer radius of the cylinder (m)
R = the radius of the cylinder or sphere (m)
Moment of Inertia Formula Questions:
1) What is the moment of inertia of a solid sphere with mass 55.0 kg, and radius 0.120 m?
Answer: The first step is to identify the correct moment of inertia formula. The moment of inertia for a solid sphere is given in the table as:
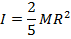
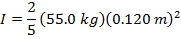
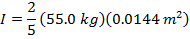
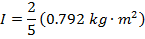
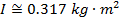
The moment of inertia of the solid sphere is 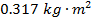 .
.
2) An empty soup can with both lids removed has a mass of 0.0580 kg, an inner radius of 0.0320 m, and an outer radius of 0.0330 m. What is the can's moment of inertia?
Answer: The first step is to identify the correct moment of inertia formula. A soup can with both lids removed is a cylinder. Since an inner and outer radius are given, the formula to use is the moment of inertia for a hollow cylinder, with a wall thickness:
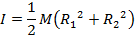
The mass of the can is M = 0.0580 kg, the inner radius is R1 = 0.0320 m, and the outer radius is R2 = 0.0330 m. The can's moment of inertia is:
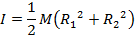
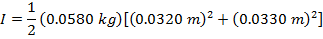

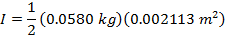
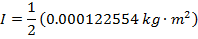
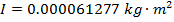
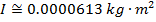
The moment of inertia of the empty soup can is approximately 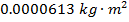 .
.
|
Related Links: |
