Magnetic Force Formula (Current-Length)
When a wire carrying electric charge is placed in a magnetic field, a force is exerted on the wire. The formula for the force depends on the current, the length of the wire, and the magnetic field. The "length vector" of the wire specifies the direction in which the current is flowing. The direction of the force vector can be found by calculating the cross product of the length vector and the magnetic field if vector directions are given, or by using the "right hand rule". Imagine your right hand with your index finger pointed in the direction of the length vector. Then, curl your fingers in the direction of the magnetic field vector. The direction of the force will be in the direction of your thumb. The unit of force is Newtons (N), the unit of current is Amperes (A), the unit of length is meters (m), and the unit of magnetic field is Teslas (T).

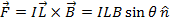
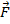 = magnetic force vector (Newtons, N)
= magnetic force vector (Newtons, N)
I = current magnitude (Amperes, A)
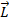 = length vector (m)
= length vector (m)
L = wire length, magnitude (m)
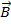 = magnetic field vector (Teslas, T)
= magnetic field vector (Teslas, T)
B = magnetic field magnitude (Teslas, T)
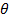 = angle between length and magnetic field vectors (radians)
= angle between length and magnetic field vectors (radians)
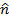 = cross product direction vector (unitless)
= cross product direction vector (unitless)
Magnetic Force Formula (Current-Length) Questions:
1) A copper wire is carrying a current of 4.00 A through a uniform magnetic field with magnitude 2.20 T. The direction of the current is from the left to right of the page (screen), and the magnetic field direction is upward-left, at an angle of 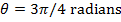 from the current direction. What is the magnitude and direction of the magnetic force acting on a 0.100 m section of the wire?
from the current direction. What is the magnitude and direction of the magnetic force acting on a 0.100 m section of the wire?
Answer: The magnitude of magnetic force on the section of wire can be found using the formula:
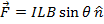
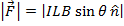
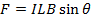
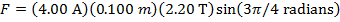
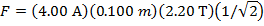
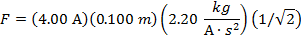
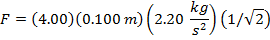
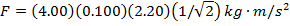
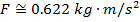
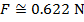
The force on a 0.100 m section of the wire has a magnitude of 0.622N.
The direction of the force vector can be found using the "right hand rule". The direction of the current is to the right, and so imagine your right index finger pointed in that direction. The magnetic field vector is pointed upward-left, so curl your fingers up. Your thumb would now be pointing away from the page (or screen). This means that the direction of the force vector is out of the page (or screen).
2) A wire is carrying a current of 20.0 A, with the current flowing the 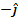 direction. A magnetic field
direction. A magnetic field 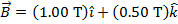 is applied to the wire. What is the resulting magnetic force acting on a 1.00 m section of the wire, expressed in unit vector notation?
is applied to the wire. What is the resulting magnetic force acting on a 1.00 m section of the wire, expressed in unit vector notation?
Answer: The magnetic force on the wire can be found by solving the cross product form of the force formula:
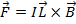
The cross product of two vectors, 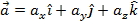 and
and 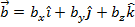 , is:
, is:
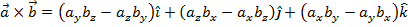
The length vector is:
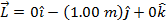
The magnetic field vector is:
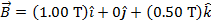
So, 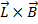 is:
is:
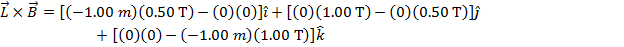
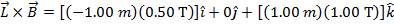
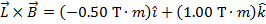
The magnetic force on the wire can now be calculated using the formula:
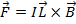
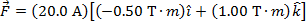
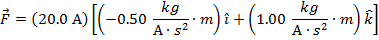
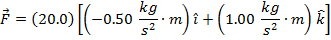
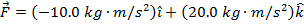
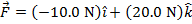
In unit vector notation, the magnetic force on the wire is 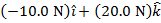 .
.
|
Related Links: |
