Magnetic Force Formula (Charge-Velocity)

When a charged particle moves in a magnetic field, a force is exerted on the moving charged particle. The formula for the force depends on the charge of the particle, and the cross product of the particle's velocity and the magnetic field. The direction of the force vector can be found by calculating the cross product if vector directions are given, or by using the "right hand rule". Imagine your right hand with your index finger pointed in the direction of the particle's velocity vector. Then, curl your fingers in the direction of the magnetic field vector. The direction of your thumb is the direction of the cross product of the vectors. If the charge is positive, the direction of the force will be in the direction of your thumb. If the charge is negative, the direction of the force will be the opposite. The unit of force is Newtons (N), the unit of charge is Coulombs (C), the unit of velocity is meters per second (m/s), and the unit of magnetic field is Teslas (T).

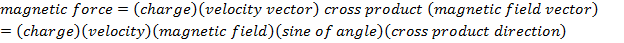
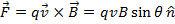
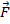= magnetic force vector (Newtons, N)

q = charge of a moving particle (Coulombs, C)

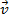= particle velocity vector (m/s)

v = particle velocity magnitude (m/s)

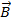= magnetic field vector (Teslas, T)

B = magnetic field magnitude (Teslas, T)

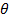= angle between velocity and magnetic field vectors (radians)

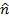= cross product direction vector (unitless)

Magnetic Force Formula (Charge-Velocity) Questions:

1) A beam of protons, each with charge 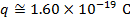, is moving at 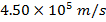through a uniform magnetic field with magnitude 0.60T. The direction of motion of the protons is to the right of the page (screen), and the magnetic field direction is downward-right, at an angle of 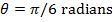from the proton direction. What is the magnitude and direction of the magnetic force acting on each proton?

Answer: The magnitude of magnetic force on a proton can be found using the formula:

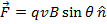
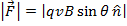
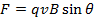
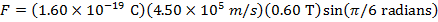
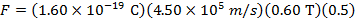
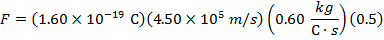
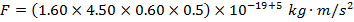
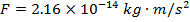
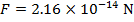
The force on each proton has a magnitude of .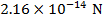

The direction of the force vector can be found using the "right hand rule". The direction of the motion of the protons is to the right, and so imagine your right index finger pointed in that direction. The magnetic field vector is pointed downward right, so curl your fingers down. Your thumb would now be pointing into the page (or screen). Since the charge of the protons is positive, this is the direction of the force vector.

2) An oil droplet with charge 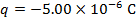is moving with velocity 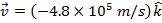. A magnetic field is applied to the droplet with magnitude and direction 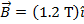. What is the resulting magnetic force that acts on the oil droplet, expressed in unit vector notation?

Answer: The magnetic force on the oil droplet can be found by solving the cross product form of the force formula:

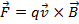
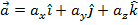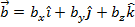The cross product of two vectors, and , is:

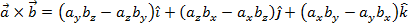
The velocity vector is:

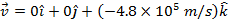
The magnetic field vector is:

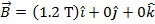
So, 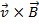is:

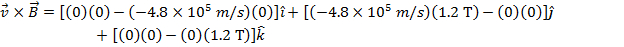
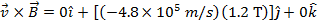
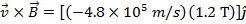
The magnetic force on the oil droplet can now be calculated using the formula:

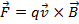
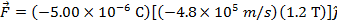
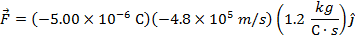
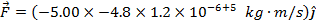
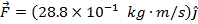
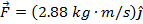
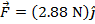
The magnetic force on the oil droplet is , meaning it has a magnitude of 2.88N in the 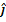direction.