Linear acceleration Formula
Before defining the linear or tangential acceleration it is necessary to first clarify that it is a term related to the circular movement; it describes a circular path around an axis on which it rotates maintaining a constant radius. When the speed of this movement is also maintained in time, what is known as uniform circular movement takes place. When a circular movement is made, the moving body has an angular velocity, since it rotates constantly with a certain inclination. The elements that compose its definition are the rotation angle for each time unit. Tangential velocity is the velocity presented by the body at a given moment in time, taking into account its direction and sense, as well as the radius by which it is traveling in a particular fraction of its trajectory. Tangential acceleration is the magnitude that links the variation of speed with time.
tangential acceleration = angular velocity / time * circle radius.
The equation is:
We have:
at = tangential acceleration.
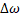= angular velocity
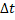= time.
r = circle radius.
Linear acceleration Questions:
1)Calculate the linear acceleration of a circular path with radius 6 m that has an initial angular velocity of 6 rad/s and a final angular velocity of 9 rad/s whose variation was made in 15 seconds.
Answer: Let's calculate the variation of angular velocity in time, for that, we calculate first the variation of angular velocity and then we apply the equation of linear acceleration.
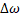= 9rad/s - 6 rad/s = 3rad/s.
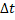= 15 s.
r = 6 m
= (3 rad/s / 15 sec)* 6 m = 1.2 m/s2
at = 1.2 m/s2.
2)What is the final angular velocity of an object moving on a circular path of radius 10 m if its tangential acceleration is 2 m/s2 and part of rest in a time of 20 seconds?
Answer: Using the tangential acceleration equation we can determine the value of the final velocity.
at = ω * r / t →
ω = at * t/ r = (2 m/s2*20 s) / 10 m = 4 rad / s
|
Related Links: |