Horizontal Range Formula

A projectile is an object that is given an initial velocity, and is acted on by gravity. The horizontal range of a projectile is the distance along the horizontal plane it would travel, before reaching the same vertical position as it started from. The horizontal range depends on the initial velocity v₀, the launch angle θ, and the acceleration due to gravity. The unit of horizontal range is meters (m).

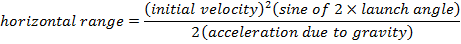
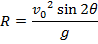
R = horizontal range (m)

v₀ = initial velocity (m/s)

g = acceleration due to gravity (9.80 m/s²)

θ = angle of the initial velocity from the horizontal plane (radians or degrees)

Horizontal Range Formula Questions:

1) A motorcyclist has set up a stunt with a ramp at the edge of a gorge 75.0 m wide. The ramp is inclined at 53.1° from the horizontal plane. She plans to take off from the ramp at a velocity of 28.0 m/s. At that velocity, what will be her horizontal range, and will she make it to the other side of the gorge?

Answer: The motorcyclist's horizontal range can be found using the formula:

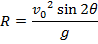
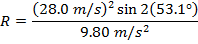
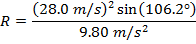
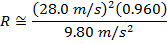
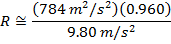
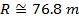
The motorcyclist's horizontal range will be 76.8 m, if she takes off from the ramp at 28.0 m/s. This is slightly greater than the 75.0 m width of the gorge, so she will make it to the other side.

2) A pirate fired one of the ship's cannons to test its range. The cannon was set at an angle of 18.5°. The pirate watched the cannon ball, and noted that it hit the water 800 m away. What was the cannon ball's velocity when it left the cannon?

Answer: The velocity of the cannon ball can be found by rearranging the horizontal range formula:

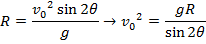
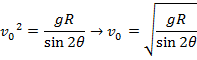
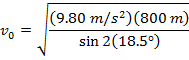
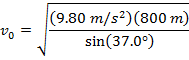
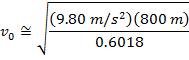
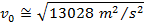
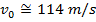
The initial velocity of the cannon ball is approximately 114 m/s.