De Broglie Wavelength Formula

In some situations, light behaves like a wave, while in others, it behaves like particles. The particles of light are called photons, and they can be thought of as both waves and particles. Louis de Broglie (1892-1987) developed a formula to relate this dual wave and particle behavior. It can also be applied to other particles, like electrons and protons. The formula relates the wavelength to the momentum of a wave/particle.

For particles with mass (electrons, protons, etc., but not photons), there is another form of the de Broglie wavelength formula. At non-relativistic speeds, the momentum of a particle is equal to its rest mass, m, multiplied by its velocity, v.

The unit of the de Broglie wavelength is meters (m), though it is often very small, and so expressed in nanometers (1 nm = 10^(-9) m), or Angstroms ().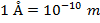

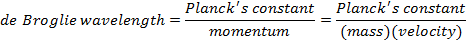
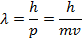
λ = the de Broglie wavelength (m)

h = Planck's constant ()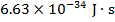

p = momentum of a particle ()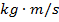

m = mass of a particle (kg)

v = velocity of a particle (m/s)

De Broglie Wavelength Formula Questions:

1) A certain photon has momentum 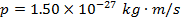. What is the photon's de Broglie wavelength?

Answer: The de Broglie wavelength of the photon can be found using the formula:

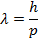
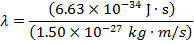
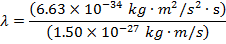
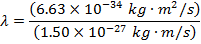
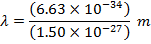
λ = 4.42 x 10^(-7) m

λ = 442 x 10^(-9) m

λ = 442 nm

The de Broglie wavelength of the photon is 442 nm. This wavelength is in the blue-violet part of the visible light spectrum.

2) The de Broglie wavelength of a certain electron is 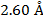. The mass of an electron is m_e = 9.109 x 10^(-31) kg. What is the magnitude of the velocity of this electron?

Answer: The magnitude of the velocity of this electron can be found by rearranging the de Broglie wavelength formula.

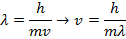
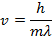
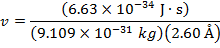
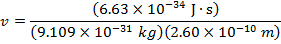
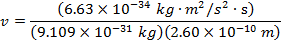
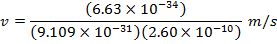
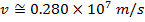
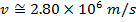
The electron with de Broglie wavelength 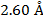has a velocity value of 2.80 x 10⁶ m/s.