Capacitance Formula

Electrical capacitance is a property of objects that can hold electric charge. A capacitor is an electric component that results from creating a small gap between charge-carrying layers, for example, a parallel-plate capacitor. The capacitance is the collected charge divided by the voltage difference across the capacitor. Capacitance is measured in Farads (F), charge is measured in Coulombs (C), and voltage is measured in Volts (V). Be careful not to confuse capacitance: C, and the unit Coulombs: C.

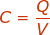
C = capacitance (Farads, F)

Q = the charge built up on the capacitor (Coulombs, C)

V = voltage difference between two sides of a capacitor (Volts, V)

Capacitance Formula Questions:

1) In an electric circuit, a capacitor is holding a charge of 0.500 C. The voltage difference across the capacitor is 5.00 V. What is the capacitance?

Answer: The capacitance can be found using the formula:

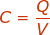
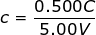
C = 0.100 F

The capacitance is 0.100 F, which can also be written in milli-Farads: 100 mF.

2) The charge held on a small parallel-plate capacitor is 100 μC (micro-Coulombs). The voltage difference across the capacitor is 20.0 mV (milliVolts). What is the capacitance?

Answer: The charge is given in units of μC. One micro-Coulomb is equal to one one-millionth of a Coulomb: 1 μC = 1/1000000C. The voltage is given in units of mV. One milliVolt is equal to one one-thousandth of a Volt: 1 mV = 1/1000 V. Using these values, the capacitance can be found using the formula:

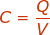
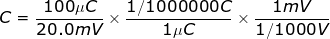
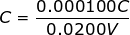
C = 0.00500 F

The capacitance is 0.00500 F, which can also be written in milli-Farads: 5.00 mF.